Question

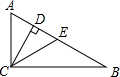在Rt△ABC，∠ACB=90°，CD、CE是斜边上的高和中线，AC=CE=10cm，则BD长为（　　）

A．25cm

B．5cm

C．15cm

D．10cm

Answer 1

分析：由直角三角形斜边上中线求得CE=

1

2

AB，则AC=

1

2

AB，所以∠B=30°；然后通过解直角三角形BCD即可求得线段BD的长度．

解答：解：∵在Rt△ABC，∠ACB=90°，CE是斜边上的中线，
∴CE=

1

2

AB．
又∵AC=CE=10cm，
∴AC=

1

2

AB，
∴∠B=30°．
∴BC=AC•cotB=10

3

cm．
∵CD是Rt△ABC斜边上的高，
∴∠CDB=90°，
∴BD=BC•cosB=10

3

×

3

2

=15cm；
故选C．

点评：本题考查了解直角三角形、含30度角的直角三角形以及直角三角形斜边上的中线．在求BC边的长度时，也可以在直角三角形ABC中利用勾股定理来求．