题目内容
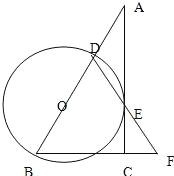
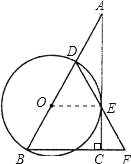
【题目】在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,连接DE并延长,与BC的延长线交于点F.
(1)求证:BD=BF;
(2)若BC=6,AD=4,求⊙O的面积.
【答案】(1)证明详见解析;(2)16π.
【解析】
试题分析:(1)作辅助线,连接OE,根据切线的性质知OE⊥AC,已知∠ACB=90°,可知OE∥BC,得∠OED=∠F,再根据OD=OE,可知∠ODE=∠OED,从而可得∠ODE=∠F,BD=BF;
(2)根据△AOE∽△ABC,可将⊙O的半径求出,代入圆的面积公式![]() ,计算即可.
,计算即可.
试题解析:(1)证明:如图,连接OE,
∵AC切⊙O于E,
∴OE⊥AC,
又∠ACB=90°,即BC⊥AC,
∴OE∥BC,
∴∠OED=∠F,
又OD=OE,
∴∠ODE=∠OED,
∴∠ODE=∠F,
∴BD=BF;
(2)解:设⊙O半径为r,
由OE∥BC得△AOE∽△ABC,
∴![]() ,即
,即![]() ,
,
∴![]() ﹣r﹣12=0,
﹣r﹣12=0,
解之得![]() =4,
=4,![]() =﹣3(舍),
=﹣3(舍),
经检验,r=4是原分式的解.
∴![]() 16π.
16π.

练习册系列答案
相关题目
【题目】某专卖店专营某品牌的衬衫,店主对上一周中不同尺码的衬衫销售情况统计如下:
尺码 | 39 | 40 | 41 | 42 | 43 |
平均每天销售数量/件 | 10 | 12 | 20 | 12 | 12 |
该店主决定本周进货时,增加一些41码的衬衫,影响该店主决策的统计量是( )
A. 平均数 B. 方差 C. 众数 D. 中位数