题目内容
【题目】已知:如图,在△ABC中,∠A=90°,AB = AC,BD平分∠ABC。
求证:BC = AB + AD

【答案】证明见解析
【解析】试题分析: 过D作DE垂直于BC,由DA垂直于AB,且BD为角平分线,利用角平分线性质得出DA=DE,再由斜边BD为公共边,利用HL得出直角三角形ABD与直角三角形BED全等,由全等三角形的对应边相等得出AB=BE,由AB=AC,且BA与AC垂直得到三角形ABC为等腰直角三角形,可得出三角形DEC为等腰直角三角形,得出DE=EC,而BC=EB+EC,等量代换即可得证.
试题解析:
过D作DE⊥BC,交BC于点E,
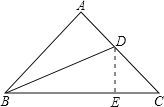
∵∠A=90,
∴DA⊥AB,
∵BD是∠ABC的平分线,DA⊥AB,DE⊥BC,
∴DA=DE,
在Rt△ABD和Rt△EBD中,
{BD=BDDA=DE,
∴Rt△ABD≌Rt△EBD(HL),
∴AB=BE,
又∵∠A=90,且AB=AC,
∴△ABC为等腰直角三角形,
∴∠C=∠ABC=45,又∠DEC=90,
∴△DEC为等腰直角三角形,
∴DE=EC,
∴AD=EC,
则BC=BE+EC=AB+AD.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目