题目内容
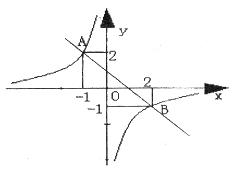
如图所示的曲线是函数y=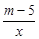 (m为常数)图象的一支.
(m为常数)图象的一支.

(1)求常数m的取值范围;
(2)若该函数的图象与正比例函数y=2x的图象在第一象限的交点为A(2,n),求点A的坐标及反比例
函数的解析式.
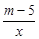 (m为常数)图象的一支.
(m为常数)图象的一支.
(1)求常数m的取值范围;
(2)若该函数的图象与正比例函数y=2x的图象在第一象限的交点为A(2,n),求点A的坐标及反比例
函数的解析式.
(1) m>5(2) 点A的坐标为(2,4);反比例函数的解析式为y=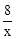
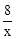
解:(1)∵函数y=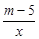 (m为常数)图象的一支在第一象限,
(m为常数)图象的一支在第一象限,
∴m-5>0,解得m>5。
(2)∵函数y=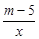 的图象与正比例函数y=2x的图象在第一象限的交点为A(2,n),
的图象与正比例函数y=2x的图象在第一象限的交点为A(2,n),
∴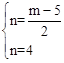 ,解得
,解得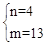 。
。
∴ 点A的坐标为(2,4);反比例函数的解析式为y=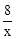 。
。
(1)曲线函数y=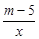 (m为常数)图象的一支在第一象限,则比例系数m-5一定大于0,即可求得m的范围。
(m为常数)图象的一支在第一象限,则比例系数m-5一定大于0,即可求得m的范围。
(2)把A的坐标代入正比例函数解析式,即可求得A的坐标,再代入反比例函数解析式即可求得反比例函数解析式。
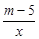 (m为常数)图象的一支在第一象限,
(m为常数)图象的一支在第一象限,∴m-5>0,解得m>5。
(2)∵函数y=
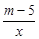 的图象与正比例函数y=2x的图象在第一象限的交点为A(2,n),
的图象与正比例函数y=2x的图象在第一象限的交点为A(2,n),∴
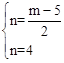 ,解得
,解得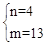 。
。∴ 点A的坐标为(2,4);反比例函数的解析式为y=
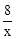 。
。(1)曲线函数y=
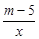 (m为常数)图象的一支在第一象限,则比例系数m-5一定大于0,即可求得m的范围。
(m为常数)图象的一支在第一象限,则比例系数m-5一定大于0,即可求得m的范围。(2)把A的坐标代入正比例函数解析式,即可求得A的坐标,再代入反比例函数解析式即可求得反比例函数解析式。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 的—次函数
的—次函数 =
= 和反比例函数
和反比例函数 的图象都经过点(1,-2).求:
的图象都经过点(1,-2).求: 的图象经过点P,则k= .
的图象经过点P,则k= .
 的图象经过点(3,-2),则k的值是 ( )
的图象经过点(3,-2),则k的值是 ( )
 图象上有三个点
图象上有三个点 ,
, ,
, ,其中
,其中 ,则
,则 ,
, ,
, 的大小关系是( )
的大小关系是( ) B.
B. C.
C. D.
D.
 的图象上有两点A(
的图象上有两点A( ),B(
),B( ),且
),且 ,那么下列结论正确的是
,那么下列结论正确的是 <
<
 上,点B在双曲线
上,点B在双曲线 上,且AB∥x轴,点C、D在x轴上,若四边形ABDC为矩形, 则它的面积为
上,且AB∥x轴,点C、D在x轴上,若四边形ABDC为矩形, 则它的面积为 