题目内容
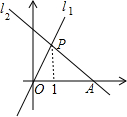 如图,直线l1:y=2x与直线l2:y=kx+3在同一平面直角坐标系内交于点P.
如图,直线l1:y=2x与直线l2:y=kx+3在同一平面直角坐标系内交于点P.(1)写出不等式2x>kx+3的解集:
(2)设直线l2与x轴交于点A,求△OAP的面积.
分析:(1)求不等式2x>kx+3的解集就是求当自变量x取什么值时,y=2x的函数值大;
(2)求△OAP的面积,只要求出OA边上的高就可以,即求两个函数的交点的纵坐标的绝对值.
(2)求△OAP的面积,只要求出OA边上的高就可以,即求两个函数的交点的纵坐标的绝对值.
解答:解:(1)从图象中得出当x>1时,直线l1:y=2x在直线l2:y=kx+3的上方,
∴不等式2x>kx+3的解集为:x>1;
(2)把x=1代入y=2x,得y=2,
∴点P(1,2),
∵点P在直线y=kx+3上,
∴2=k+3,
解得:k=-1,
∴y=-x+3,
当y=0时,由0=-x+3得x=3,
∴点A(3,0),
∴S△OAP=
×3×2=3.
∴不等式2x>kx+3的解集为:x>1;
(2)把x=1代入y=2x,得y=2,
∴点P(1,2),
∵点P在直线y=kx+3上,
∴2=k+3,
解得:k=-1,
∴y=-x+3,
当y=0时,由0=-x+3得x=3,
∴点A(3,0),
∴S△OAP=
| 1 |
| 2 |
点评:求线段的长度的问题一般是转化为求点的坐标的问题来解决.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 20、如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,3),则关于x的不等式x+1≥mx+n的解集为
20、如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,3),则关于x的不等式x+1≥mx+n的解集为 如图,直线l1、l2交于点A,试求点A的坐标.
如图,直线l1、l2交于点A,试求点A的坐标. 如图,直线l1:y=2x+4与l2:y=-x-5在同一平面角坐标系中相交于点P,则点P的坐标是
如图,直线l1:y=2x+4与l2:y=-x-5在同一平面角坐标系中相交于点P,则点P的坐标是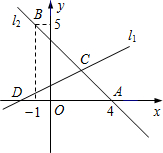 l2交于点C.
l2交于点C. 如图,直线l1,l2交于点A,直线l2与x轴交于点B,与y轴交于点D,直线l1所对应的函数关系式为y=-2x+2.
如图,直线l1,l2交于点A,直线l2与x轴交于点B,与y轴交于点D,直线l1所对应的函数关系式为y=-2x+2.