题目内容
如图,直线l1的解析表达式为y=| 1 | 2 |
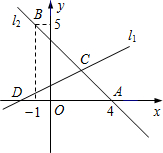 l2交于点C.
l2交于点C.(1)求直线l2的函数关系式;
(2)求△ADC的面积;
(3)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.
分析:(1)设出直线l2的函数关系式,因为直线过A(4,0),B(-1,5)两点利用代入法求出k,b,从而得到关系式.
(2)首先求出D,C两点的坐标,D点坐标是l1与x轴的交点坐标,C点坐标是把l1,l2联立,求其方程组的解再求三角形的面积.
(3)另有一点P,由于△ADP与△ADC的面积相等,所以△ADP的面积为6,因为AD长是6,所以P点纵坐标是-2,再根据P在l2上,求其横坐标.
(2)首先求出D,C两点的坐标,D点坐标是l1与x轴的交点坐标,C点坐标是把l1,l2联立,求其方程组的解再求三角形的面积.
(3)另有一点P,由于△ADP与△ADC的面积相等,所以△ADP的面积为6,因为AD长是6,所以P点纵坐标是-2,再根据P在l2上,求其横坐标.
解答:解:(1)设l2的函数关系式为:y=kx+b,
∵直线过A(4,0),B(-1,5),
∴
,
解得;
,
∴l2的函数关系式为:y=-x+4;
(2)∵l1的解析表达式为y=
x+1,
∴D点坐标是;(-2,0),
∵直线l1与l2交于点C.
∴
,
解得;
,
∴C(2,2),
△ADC的面积为:
×AD×2=
×6×2=6;
(3)∵△ADP与△ADC的面积相等,
∴△ADP的面积为6,
∵AD长是6,
∴P点纵坐标是-2,
再根据P在l2上,则-2=-x+4,解得:x=6,其横坐标为6,故P点坐标为:(6,-2).
∵直线过A(4,0),B(-1,5),
∴
|
解得;
|
∴l2的函数关系式为:y=-x+4;
(2)∵l1的解析表达式为y=
| 1 |
| 2 |
∴D点坐标是;(-2,0),
∵直线l1与l2交于点C.
∴
|
解得;
|
∴C(2,2),
△ADC的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
(3)∵△ADP与△ADC的面积相等,
∴△ADP的面积为6,
∵AD长是6,
∴P点纵坐标是-2,
再根据P在l2上,则-2=-x+4,解得:x=6,其横坐标为6,故P点坐标为:(6,-2).
点评:此题主要考查了代定系数法求函数关系式,求函数与坐标轴的交点,与两个函数的交点问题,题目综合性较强,难度不大,比较典型.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
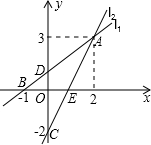 的交点为C(0,-2),直线l1、l2相交于点A,结合图象解答下列问题:
的交点为C(0,-2),直线l1、l2相交于点A,结合图象解答下列问题: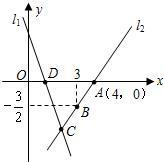 如图,直线l1的解析表达式为y=-3x+3,l1与x轴交于点D,直线l2经过点A,B,且直线l1,l2交于点C.
如图,直线l1的解析表达式为y=-3x+3,l1与x轴交于点D,直线l2经过点A,B,且直线l1,l2交于点C. l2交于点C.
l2交于点C. 如图,直线l1的解析表达式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,
如图,直线l1的解析表达式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,