题目内容
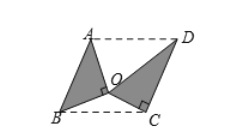
【题目】如图，把含
角的两块直角三角板放置在同一平面内，若
则以
为顶点的四边形的面积是_____．
【答案】
【解析】
延长CO，交AB于点E，根据平行四边形的判定可得四边形ABCD为平行四边形，然后根据平行四边形的面积公式和三角形的面积公式证出S平行四边形ABCD=2（S△AOB＋S△COD），再求出OA、OB和OC，即可求出S△AOB和S△COD，从而求出结论．
解：延长CO，交AB于点E，由题意可知：∠BAO=45°，∠CDO=30°
∵
∴四边形ABCD为平行四边形
∵OC⊥CD
∴CE⊥AB
∴S△AOB＋S△COD=
AB·OE＋CD·OC
=AB·（OE＋OC）
=AB·CE
=S平行四边形ABCD
∴S平行四边形ABCD=2（S△AOB＋S△COD）
在Rt△AOB中，AO2＋BO2=AB2=6,AO=BO
解得:AO=BO=
在Rt△COD中，∠CDO=30°,OC2＋CD2=OD2
∴OD=2OC, OC2＋6=(2OC)2
解得:OC=
，
∴S△AOB=AO·BO=
，S△COD=CD·OC=
∴S平行四边形ABCD=2（S△AOB＋S△COD）
=2×（＋）
=
故答案为：．
练习册系列答案
名校课堂系列答案
相关题目
