Question

【题目】一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形，边长都为1，则扇形和圆形纸板的面积比是（ ）
A.5：4
B.5：2
C. ：2
D. ：

Answer 1

【答案】A
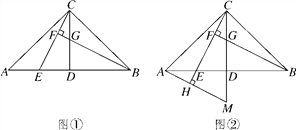
【解析】解：如图1，连接OD， ∵四边形ABCD是正方形，
∴∠DCB=∠ABO=90°，AB=BC=CD=1，
∵∠AOB=45°，
∴OB=AB=1，
由勾股定理得：OD= = ，
∴扇形的面积是 = π；
如图2，连接MB、MC，
∵四边形ABCD是⊙M的内接四边形，四边形ABCD是正方形，
∴∠BMC=90°，MB=MC，
∴∠MCB=∠MBC=45°，
∵BC=1，
∴MC=MB= ，
∴⊙M的面积是π×（ ）2= π，
∴扇形和圆形纸板的面积比是 π÷（ π）= ．
故选：A．

【考点精析】本题主要考查了勾股定理的概念和正多边形和圆的相关知识点，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角；圆的外切四边形的两组对边的和相等才能正确解答此题．