��Ŀ����
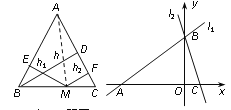
����Ŀ���Ķ����⣺���á�ͬһͼ�ε������ȡ�����֤��һЩ�����߶εĵ�ʽ���������ֽ������ķ������dz�֮Ϊ�����. ��ͼ1���ڵ�����ABC�У�AB=AC�� AC���ϵĸ�Ϊh����MΪ�ױ�BC�ϵ�����һ�㣬��M����AB��AC�ľ���ֱ�Ϊh1��h2������AM������S��ABC=S��ABM��S��ACM�����Եó����ۣ�h= h1��h2.
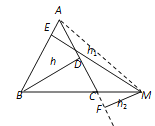
���̽������ͼ1�У�����M��BC���ӳ�����ʱ������h��h1��h2֮���������ϵ��֤����Ľ���.
��չӦ�ã���ͼ2����ƽ��ֱ������ϵ�У�������ֱ��l1��y =![]() x+3��l2��y =��3x+3����l2��һ��M��l1�ľ�����1�������� ���Ķ����⡱�͡����̽�����л�õĽ��ۣ������M������.
x+3��l2��y =��3x+3����l2��һ��M��l1�ľ�����1�������� ���Ķ����⡱�͡����̽�����л�õĽ��ۣ������M������.
���𰸡���1��h = h1��h2��2����![]() ��2����
��2����![]() ��4��
��4��
�������������������1������AM����ABC���ֳɡ�ABM�͡�ACM���������Σ����������ε������ʽ�ֱ���⣬�ٸ���S��ABC=S��ABM+S��AMC�������ɵõ�h1+h2=h��
��2���ȸ���ֱ�߹�ϵʽ���A��B��C������������ù��ɶ������AB=AC�����ԡ�ABC�ǵ��������Σ��ٷֵ�M���߶�BC�Ϻ�CB���ӳ������������������⣮
���������
��1��h = h1��h2.
֤��������OA��
��S��ABC =![]() AC��BD=
AC��BD=![]() AC��h��
AC��h��
S��ABM =![]() AB��ME =
AB��ME = ![]() AB��h1��
AB��h1��
S��ACM=![]() AC��MF =
AC��MF =![]() AC��h2��.
AC��h2��.
�֡�S��ABC=S��ABM��S��ACM��
��![]() AC��h =
AC��h =![]() AB��h1��
AB��h1��![]() AC��h2.
AC��h2.
��AB=AC����h = h1��h2.
��2����y =![]() x+3����x=0��y=3����y=0��x=��4����
x+3����x=0��y=3����y=0��x=��4����
A����4��0����B��0��3�� �� ͬ�����C��1��0����
OA=4��OB=3�� AC=5��
AB=![]() =5������AB=AC��
=5������AB=AC��
����ABC����������
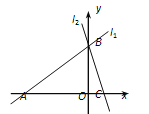
���M��������x��y����
�ٵ���M��BC����ʱ����h1+h2=h�ã�
OB = 1+y��y =3��1=2����������y=��3x+3����ã�x=![]() ��
��
��M��![]() ��2��
��2��
�ڵ���M��CB�ӳ�����ʱ����h1��h2=span>h�ã�
OB = y��1��y =3+1=4����������y=��3x+3����ã�x=��![]() ��
��
��M����![]() ��4��.
��4��.
����������M��������![]() ��2����
��2����![]() ��4��.
��4��.