题目内容
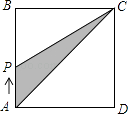
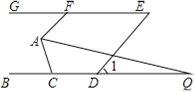
【题目】如图,已知△ABC与△CDE都是等边三角形,点B、C、D在同一直线上,AD与BE相交于点G,BE与AC相交于点F,AD与CE相交于点H,则下列结论:①△ACD≌△BCE;②∠AGB=60°;③BF=AH;④△CFH是等边三角形;⑤连CG,则∠BGC=∠DGC ;⑥EG+GC=GD. 其中正确的有________.(只要写序号)

【答案】①②③④⑤⑥
【解析】
利用等边三角形的性质得出条件,可证明:△BCE≌△ACD;利用△BCE≌△ACD得出∠CBF=∠CAH,再运用平角定义得出∠BCF=∠ACH,进而得出△BCF≌△ACH因此BF=AH.由CF=CH和∠ACH=60°根据“有一个角是60°的三角形是等边三角形可得△CFH是等边三角形.连接CG,过C作CI⊥BE于I,CJ⊥AD于J.由全等三角形对应边上的高相等得到CI=CJ,由角平分线的判定定理得到GC平分∠BGD.
在GD上截取GM=GE,连接EM.由∠EGM=∠AGB=60°,得到△EGM是等边三角形,得到ME=GE,∠GEM=60°.通过证明△GEC≌△MED,得到GC=MD,即可得到GD=GM+MD=GE+CG.
∵∠BCA=∠DCE=60°,∴∠ACE=60°,∴∠BCE=∠ACD.在△BCE和△ACD中,∵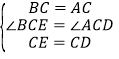 ,∴△BCE≌△ACD(SAS);故①正确;
,∴△BCE≌△ACD(SAS);故①正确;
∵△BCE≌△ACD,∴∠CBF=∠CAH.
∵∠BFC=∠AFG,∴∠AGB=∠ACB=60°,故②正确;
在△BCF和△ACH中,∵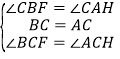 ,∴△BCF≌△ACH(ASA),∴CF=CH,BF=AH;故③正确;
,∴△BCF≌△ACH(ASA),∴CF=CH,BF=AH;故③正确;
∵CF=CH,∠ACH=60°,∴△CFH是等边三角形;故④正确;
连接CG.过C作CI⊥BE于I,CJ⊥AD于J.
∵△BCE≌△ACD,∴CI=CJ,∴GC平分∠BGD,∴∠BGC=∠DGC.故⑤正确.
在GD上截取GM=GE,连接EM.
∵∠EGM=∠AGB=60°,∴△EGM是等边三角形,∴ME=GE,∠GEM=60°.
∵∠CED=60°,∴∠GEC=∠MED.在△GEC和△MED中,∵GE=ME ,∠GEC=∠MED,CE=DE,∴△GEC≌△MED,∴GC=MD,∴GD=GM+MD=GE+CG.故⑥正确.
故答案为:①②③④⑤⑥.

【题目】下表中有两种移动电话计费方式:
月使用费(元) | 主叫限定时间(分钟) | 主叫超时费(元/分钟) | 被叫 | |
方式一 | 65 | 160 | 0.25 | 免费 |
方式二 | 100 | 380 | 0.19 | 免费 |
说明:月使用费固定收取,主叫不超限定时间不再收费,主叫超时部分加收超时费;被叫免费.
(1)若李杰某月主叫通话时间为200分钟则他按方式一计费需 元,按方式二计费需 元;若他按方式二计费需103.8元,则主叫通话时间为 分钟;
(2)是否存在某主叫通话时间t(分钟),按方式一和方式二的计费相等,若存在,请求出t的值;若不存在,请说明理由;
(3)请你通过计算分析后,直接给出当月主叫通话时间t(分钟)满足什么条件时,选择方式一省钱;当每月主叫通话时间t(分钟)满足什么条件时,选择方式二省钱.