题目内容
如图，四边形ABCD的对角线AC、BD相交于点O，△ABC≌△BAD．求证：（1）OA=OB；（2）AB∥CD．
（1）证明略
（2）证明略
（1）∵△ABC≌△BAD，∴∠CAB=∠DBA，∴OA=OB．
（2）∵△ABC≌△BAD，∴AC=BD．
又∵OA=OB，∴∠OCD=∠ODC．
∵∠AOB=∠COD，∠CAB=
，∠ACD=
，
∴∠CAB=∠ACD，
∴AB∥CD．
（2）∵△ABC≌△BAD，∴AC=BD．
又∵OA=OB，∴∠OCD=∠ODC．
∵∠AOB=∠COD，∠CAB=
，∠ACD=，∴∠CAB=∠ACD，
∴AB∥CD．
练习册系列答案
学业测评一课一测系列答案
小学课时作业全通练案系列答案
相关题目
，
，坝高DE＝6米.
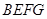、正方形
和正方形
的位置如图所示，点
在线段
上，正方形
的面积为：（ ）
的两条对角线
、
相交于点
．