题目内容
【题目】从江县盛产椪柑,春节期间,一外地运销客户安排15辆汽车装运A、B、C三种不同品质的椪柑120吨到外地销售,按计划15辆汽车都要装满且每辆汽车只能装同一种品质的椪柑,每种椪柑所用车辆都不少于3辆.
(1)设装运A种椪柑的车辆数为x辆,装运B种椪柑车辆数为y辆,根据下表提供的信息,求出y与x之间的函数关系式;
椪柑品种 | A | B | C |
每辆汽车运载量(吨) | 10 | 8 | 6 |
每吨椪柑获利(元) | 800 | 1200 | 1000 |
(2)在(1)条件下,求出该函数自变量x的取值范围,车辆的安排方案共有几种?请写出每种安排方案;
(3)为了减少椪柑积压,从江县制定出台了促进椪柑销售的优惠政策,在外地运销客户原有获利不变的情况下,政府对外地运销客户,按每吨50元的标准实行运费补贴.若要使该外地运销客户所获利润W(元)最大,应采用哪种车辆安排方案?并求出利润W(元)的最大值?
【答案】(1)y与x之间的函数关系式为y=15﹣2x;(2)有四种方案,方案一:装运A、B、C三种不同品质的车辆分别是3辆、9辆、3辆;方案二:装运A、B、C三种不同品质的车辆分别是4辆、7辆、4辆;方案三:装运A、B、C三种不同品质的车辆分别是5辆、5辆、5辆;方案四:装运A、B、C三种不同品质的车辆分别是6辆、3辆、6辆;(3)采用方案一利润W(元)的最大值是134400元.
【解析】
(1)根据一共有15辆车,要运送120吨椪柑,根据表格中的数据列式,由此可得出x与y的关系式;
(2)根据装运每种椪柑的车辆数≥3,可得关于x的不等式组,解不等式组即可求得答案;
(3)总利润为:装运A种椪柑的车辆数×10×800+装运B种椪柑的车辆数×8×1200+装运C种椪柑的车辆数×6×1000+运费补贴,然后按x的取值来判定.
(1)由题意可得,
10x+8y+6(15﹣x﹣y)=120,
化简,得
y=15﹣2x,
即y与x之间的函数关系式为y=15﹣2x;
(2)由题意可得,
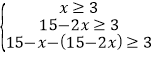 ,
,
解得,3≤x≤6,
∵x为正整数,
∴有四种方案,
方案一:装运A、B、C三种不同品质的车辆分别是3辆、9辆、3辆;
方案二:装运A、B、C三种不同品质的车辆分别是4辆、7辆、4辆;
方案三:装运A、B、C三种不同品质的车辆分别是5辆、5辆、5辆;
方案四:装运A、B、C三种不同品质的车辆分别是6辆、3辆、6辆;
(3)由题意得
W=10x×800+8(15﹣2x)×1200+6[15﹣x﹣(15﹣2x)]×1000+120×50=﹣5200x+150000,
∵-5200<0,
∴W随着x的增大而减小,
∵3≤x≤6,
∴x=3时,W取得最大值,此时W=134400,
答:采用方案一:装运A、B、C三种不同品质的车辆分别是3辆、9辆、3辆,利润W(元)的最大值是134400元.

 名校课堂系列答案
名校课堂系列答案