题目内容
已知：如图，E、F是平行四边行ABCD的对角线AC上的两点，AE=CF。
求证：（1）△ADF≌△CBE；（2）EB∥DF。
【解析】要证△ADF≌△CBE，因为AE=CF，则两边同时加上EF，得到AF=CE，又因为ABCD是平行四边形，得出AD=CB，∠DAF=∠BCE，从而根据SAS推出两三角形全等，由全等可得到∠DFA=∠BEC，所以得到DF∥EB
见解析
解析:证明：(1)∵AE=CF
∴AE+EF=CF+FE即AF=CE …………………… 1分
又ABCD是平行四边形，∴AD=CB，AD∥BC
∴∠DAF=∠BCE ……………………………2分
在△ADF与△CBE中
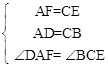…………………… 4分
∴△ADF≌△CBE（SAS）………………………5分
（2）∵△ADF≌△CBE
∴∠DFA=∠BEC ……………………………6分
∴DF∥EB……………………………………7分
练习册系列答案
相关题目
交⊙O于F，GF切⊙O于F且与CP交于G，CH切⊙O于C且与AB的延长线交于H，如果GP2=GD•GC，AD平分∠BAP并交HP于M．
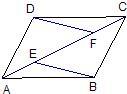24、已知：如图，E、F是四边形ABCD的对角线AC上的两点，AF=CE，DF=BE，DF∥BE．
已知：如图正方形ABCD，E是BC的中点，F在AB上，且BF=
已知：如图，A、C是?DEBF的对角线EF所在直线上的两点，且AE=CF．