Question

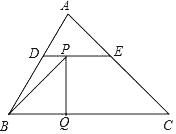
【题目】如图，△ABC 中，∠C=90°，CA=CB，D 为 AC 上的一点，AD=3CD，AE⊥AB 交 BD 延长线于 E，记△EAD，△DBC 的面积分别为 S1，S2，则 S1：S2=______．

Answer 1

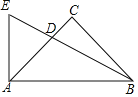
【答案】9：5

【解析】

如图，作DF∥BC交AB于F，作DH⊥AB于H．想办法证明DE：DB=3：5，推出S△ADBS1，根据，即可解决问题．

如图，作DF∥BC交AB于F，作DH⊥AB于H．

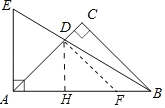
∵CA=CB，∠C=90°，∴∠CAB=∠CBA=45°．

∵DF∥BC，∴∠DFA=∠CBA=45°，∴∠DAF=∠DFA，∴DA=DF，∴DH⊥AF，∴AH=HF．

∵DF∥BC，∴3，∴．

∵DH⊥AB，AE⊥AB，∴DH∥AE，∴，∴S△ADBS1．

∵，∴，∴S1：S2=9：5．

故答案为：9：5．