题目内容
如图1,在正方形ABCD中,AB=1,点E在AB延长线上,联结CE、DE,DE交边BC于点F,设BE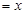 ,CF
,CF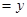 .
.
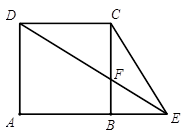
图1
(1)求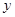 关于
关于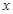 的函数解析式,并写出
的函数解析式,并写出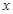 的取值范围;
的取值范围;
(2)如图2,对角线AC、BD的交点记作O,直线OF交线段CE于点G,求证: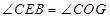 ;
;

图2
(3)在(2)的条件下,当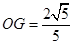 时,求
时,求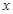 的值.
的值.
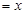 ,CF
,CF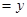 .
.
图1
(1)求
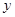 关于
关于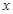 的函数解析式,并写出
的函数解析式,并写出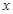 的取值范围;
的取值范围;(2)如图2,对角线AC、BD的交点记作O,直线OF交线段CE于点G,求证:
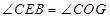 ;
;
图2
(3)在(2)的条件下,当
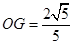 时,求
时,求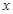 的值.
的值.(1)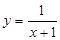
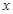 的取值范围是
的取值范围是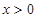
(2)略.
(3)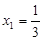 ,
,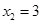
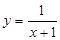
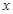 的取值范围是
的取值范围是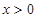
(2)略.
(3)
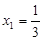 ,
,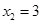
试题分析:(1)由正方形ABCD可得,
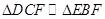 ,则
,则 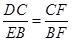 ,
,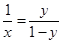
即
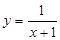
(2)由(1)的结论得:
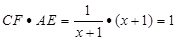
又
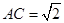
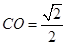
 ,即
,即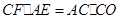 ,
,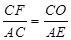
根据正方形ABCD的性质得
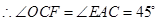 ,∴△OCF∽△EAC
,∴△OCF∽△EAC故
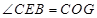 .
.(3)在
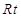 △
△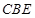 中,利用勾股定理得
中,利用勾股定理得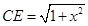
∵
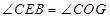 ,
,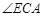 是公共角,
是公共角,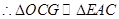 , ∴根据相似三角形的性质三边对应成比例得
, ∴根据相似三角形的性质三边对应成比例得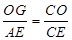 ∴
∴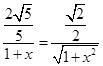
解得
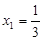 ,
,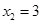
试题解析:(1)正方形ABCD中,DC∥AB,
∴
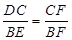 , 即
, 即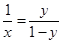 . (2分)
. (2分)∴
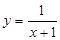
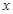 的取值范围是
的取值范围是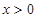 ; (2分)
; (2分)(2)∵
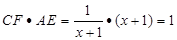 ,
,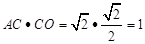
∴
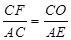 (2分)
(2分)又∵
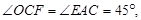
∴△OCF∽△EAC (2分)
∴
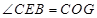 (1分)
(1分)(3)在
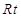 △
△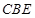 中,
中,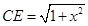 (1分)
(1分)∵
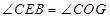 ,
,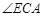 是公共角,
是公共角,∴△OCG∽ △ECA (2分)
∴
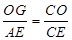
∴
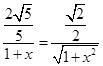 , 解得
, 解得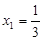 ,
,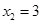 (2分)
(2分)经检验
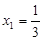 ,
,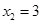 都是满足方程的解
都是满足方程的解答(略)

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
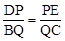
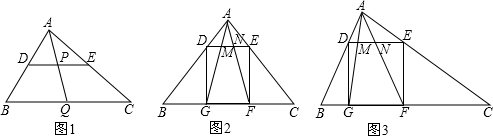
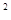 =DM·EN
=DM·EN
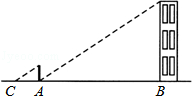
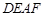 内接于△
内接于△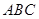 ,已知
,已知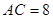 ,
,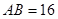 ,那么正方形的边长是 .
,那么正方形的边长是 .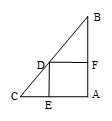
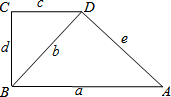
 ,则△EFC的周长为【 】
,则△EFC的周长为【 】
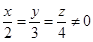 ,则
,则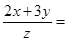 .
.