��Ŀ����
����Ŀ�������������
ѧϰ��������ȫ�ȵ��ж�����������SAS������ASA������AAS������SSS������ֱ��������ȫ�ȵ��ж�����������HL���������Ǽ����ԡ������������������ߺ�����һ�ߵĶԽǶ�Ӧ��ȡ������ν����о���
������˼����
���Dz����������÷������Ա�ʾΪ���ڡ�ABC�͡�DEF�У�AC=DF��BC=EF����B=��E��Ȼ�ԡ�B���з��࣬�ɷ�Ϊ����B��ֱ�ǡ��۽ǡ���ǡ������������̽����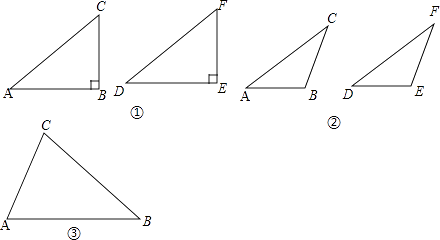
������̽����
��һ�����������B��ֱ��ʱ����ABC�ա�DEF��
��1����ͼ�٣��ڡ�ABC�͡�DEF��AC=DF��BC=EF����B=��E=90�㣬���� �� ����֪��Rt��ABC��Rt��DEF��
�ڶ������������B�Ƕ۽�ʱ����ABC�ա�DEF��
��2����ͼ�ڣ��ڡ�ABC�͡�DEF��AC=DF��BC=EF����B=��E���ҡ�B����E���Ƕ۽ǣ���֤����ABC�ա�DEF��
���������������B�����ʱ����ABC�͡�DEF��һ��ȫ�ȣ�
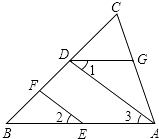
��3���ڡ�ABC�͡�DEF��AC=DF��BC=EF����B=��E���ҡ�B����E������ǣ������ó߹���ͼ����������DEF��ʹ��DEF�͡�ABC��ȫ�ȣ�����д������������ͼ�ۼ���
��4����B��Ҫ����ʲô�������Ϳ���ʹ��ABC�ա�DEF����ֱ��д�����ۣ��ڡ�ABC�͡�DEF�У�AC=DF��BC=EF����B=��E���ҡ�B����E������ǣ��� �� ���ABC�ա�DEF��
���𰸡�
��1��HL
��2��
֤������ͼ�ڣ�����C��CG��AB��AB���ӳ�����G������F��FH��DE��DE���ӳ�����H��
�ߡ�ABC=��DEF���ҡ�ABC����DEF���Ƕ۽ǣ�
��180�㩁��ABC=180�㩁��DEF��
����CBG=��FEH��
�ڡ�CBG�͡�FEH�У�
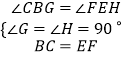 ��
��
���CBG�ա�FEH��AAS����
��CG=FH��
��Rt��ACG��Rt��DFH��
![]() ��
��
��Rt��ACG��Rt��DFH��HL����
���A=��D��
�ڡ�ABC�͡�DEF�У�
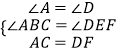 ��
��
���ABC�ա�DEF��AAS����
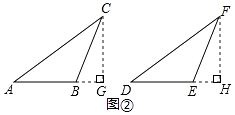
��3��
�⣺��ͼ���У��ڡ�ABC�͡�DEF��AC=DF��BC=EF����B=��E��
��DEF�͡�ABC��ȫ�ȣ�
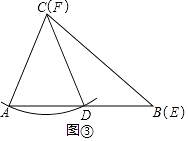
��4����B�ݡ�A
����������1.���⣺��ͼ�٣�
�ߡ�B=��E=90�㣬
����Rt��ABC��Rt��DEF��![]() ��
��
��Rt��ABC��Rt��DEF��HL����
�ʴ�Ϊ��HL��
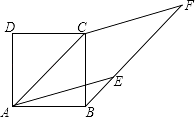
��4.���⣺��ͼ�ۿ�֪����A=��CDA=��B+��BCD��
���A����B��
�൱��B�ݡ�Aʱ����ABC��Ψһȷ���ˣ�
���ABC�ա�DEF��
�ʴ�Ϊ����B�ݡ�A��
��1��ֱ������HL�����ó�Rt��ABC��Rt��DEF����2�����ȵó���CBG�ա�FEH��AAS������CG=FH�������ó�Rt��ACG��Rt��DFH���������ABC�ա�DEF����3��������֪ͼ������һ���۽������μ��ɵó��𰸣���4�����ã�3���з����ɵó�����B�ݡ�Aʱ�����ABC�ա�DEF��