题目内容
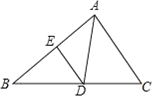
【题目】如图,△ABC中,D是BC上一点,∠DAC=∠B,E为AB上一点.
(1)求证:△CAD∽△CBA;
(2)若BD=10,DC=8,求AC的长;
(3)在(2)的条件下,若DE∥AC,AE=4,求BE的长.
【答案】(1)证明见解析;(2)12;(3)5.
【解析】试题分析:(1)有两组角对应相等的两个三角形相似,据此判断△CAD∽△CBA即可;
(2)根据相似三角形的对应边成比例,得出AC2=CD×CB,再根据BD=10,DC=8,求得AC的长即可;
(3)根据平行线分线段成比例定理,由DE∥AC,得出BE:EA=BD:DC,再根据BD=10,DC=8,AE=4,求得BE=5即可.
试题解析:解:(1)∵在△CAD和△CBA中,∠DAC=∠B,∠ACD=∠BCA,∴△CAD∽△CBA;
(2)∵△CAD∽△CBA,∴CD:AC=CA:BC,即AC2=CD×CB,又∵BD=10,DC=8,∴AC2=8×18=144,∴AC=±12,又∵AC>0,∴AC=12;
(3)∵DE∥AC,∴BE:EA=BD:DC,又∵BD=10,DC=8,AE=4,∴BE:4=10:8,∴BE=5.

练习册系列答案
相关题目