Question

【题目】如图,在△ABC中,∠ACB=90，D是BC延长线上一点，E是BD的垂直平分线与AB的交点，DE交AC于点F，求证：EA=EF.

Answer 1

【答案】详见解析.

【解析】

过E作EG垂直于AC,交AC于G,可得出EG∥BD故∠AEG=∠B, ∠D=∠DEG.再根据E是BD的垂直平分线与AB的交点可得出∠B=∠D,根据ASA定理得出△AEG≌△FEG,进而可得出结论.

证明：过E作EG垂直于AC，交AC于G，

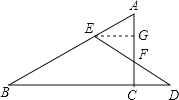
∵∠ACB=90°，

∴EG//BD，

∴∠AEG=∠B，∠D=∠DEG.

∵E是BD的垂直平分线与AB的交点，

∴BE=DE，

∴∠B=∠D，

∴∠AEG=∠DEG.

在△AEG与△FEG中，

∵∠AEG=∠FEG

EG=EG

∠AGE=∠FGE，

∴△AEG与△FEG (ASA)，

∴EA=EF.