Question

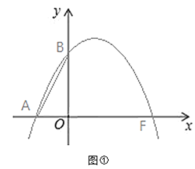
【题目】如图，已知抛物线L：y=ax2+bx+c经过点A(-3，0)、B(0，4)和F(4，0)．

　　　

(1)求抛物线L的解析式；

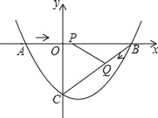
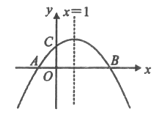
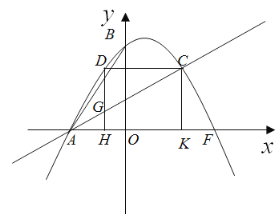
(2)在图①抛物线L上，求作点C(保留作图痕迹，不写作法)，使∠BAC=∠FAC，并求出点C的坐标；

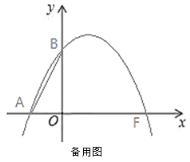
(3)在图①中，若点D为抛物线上一动点，过点D作DH⊥x轴于点H，交直线AC于点G，过点C作CK⊥x轴于点K，连接DC，当以点G，C，D为顶点的三角形与△ACK相似时，求点D的坐标．

Answer 1

【答案】（1）；（2）点C的坐标（，）；（3）点D的坐标（，）或（，）．

【解析】

（1）将点A(-3，0)、B(0，4)和F(4，0)的坐标代入解析式中即可求出结论；

（2）根据题意，作出∠BAF的角平分线AC即可，然后过点B作BP∥AC交x轴于点P，过点C作CQ⊥x轴于点Q，设点C的坐标为（t，），证出，列出比例式即可求出t，从而求出点C的坐标；

（3）根据相似三角形的对应情况分类讨论，分别画出对应的图形，然后根据抛物线的对称性、相似三角形的判定及性质和联立方程求交点坐标，即可分别求出结论．

解：（1）将点A(-3，0)、B(0，4)和F(4，0)的坐标代入抛物线L的解析式中，得

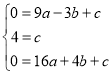
解得：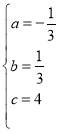

∴抛物线L的解析式为；

（2）以A为圆心，任意长度为半径作弧，分别交AB、AF于M、N；然后分别以M、N为圆心，大于的长为半径作弧，两弧交于点E，作射线AE，交y轴于点P，交抛物线于点C，易知此时AC平分∠BAF，即∠BAC=∠FAC，如下图所示，点C即为所求．

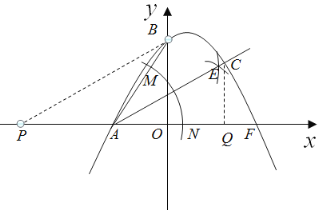
过点B作BP∥AC交x轴于点P，过点C作CQ⊥x轴于点Q

∵点A(-3，0)、B(0，4)，∠BOA=90°

∴AO=3，BO=4，

根据勾股定理可得AB=

∵BP∥AC，AC平分∠BAF

∴∠BPO=∠CAQ，∠BAO=2∠CAQ

∴∠BAO=2∠BPO

∵∠BAO=∠BPO＋∠ABP

∴∠BPO=∠ABP

∴AP=AB=5

∴PO=AP＋AO=8

设点C的坐标为（t，），由图可知：t＞0

∴OQ=t，CQ=

∴AQ=t＋3

∵∠CQA=∠BOP=90°，∠CAQ =∠BPO

∴

∴

即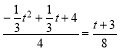

解得：（不符合t的取值范围，舍去）

∴点C的纵坐标为=

∴点C的坐标为（，）；

（3）①当时，如下图所示

∴∠DCG=∠KAC，∠CDG=∠AKC=90°

∴CD∥x轴

此时点C、D关于抛物线L的对称轴对称，对称轴为直线x==

∵点C的坐标为（，）

∴此时点D的坐标为（，）；

②当时，如下图所示

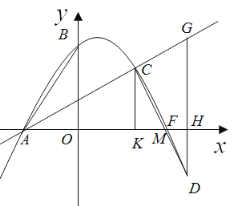
∴∠DCG=∠AKC=90°

∴DC⊥AC

设CD与x轴交于点M

由（2）知：点C的坐标为（，），AK=，CK=

∵∠AKC=∠CKM=∠ACM=90°

∴∠CAK＋∠ACK=90°，∠MCK＋∠ACK=90°

∴∠CAK=∠MCK

∴

∴

∴

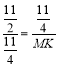
解得：MK=

∴OM=

∴点M的坐标为（，0）

设直线CD的解析式为y=kx＋d

将点C和点M的坐标代入，得

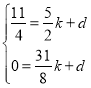
解得：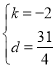

∴直线CD的解析式为

联立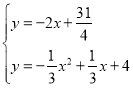

解得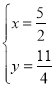：或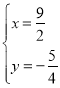

其中点C的坐标为（，）

∴点D的坐标为（，）；

③∵∠DGC一定不等于90°

∴不存在点D，使或；

当以点G，C，D为顶点的三角形与相似时，点D的坐标为（，）或（，）．