题目内容
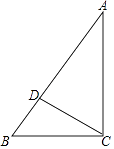
【题目】如图所示,一个四边形纸片ABCD,∠D=90°把纸片按如图所示折叠,使点B落在AD上的B′处,AE是折痕.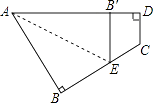
(1)若B′E∥CD,求∠B的度数.
(2)在(1)的条件下,如果∠C=128°,求∠EAB的度数.
【答案】
(1)解:∵B′E∥CD,
∴∠D=∠AB′E=90°,
∴∠B=∠AB′E=90°;
(2)解:∵B′E∥CD,
∴∠C=∠BEB′=128°
∵∠AEB=∠AEB′= ![]() ∠BEB′=64°,
∠BEB′=64°,
∵∠B=90°,
∠EAB=90°﹣∠AEB=90°﹣64°=26°.
【解析】(1)根据平行线的性质,可得∠D=∠AB′E,根据翻折的性质,可得答案;
(2)根据平行线的性质,可得∠C=∠BEB′,根据翻折的性质,可得∠AEB=∠AEB′,根据直角三角形的性质,可得答案.
【考点精析】本题主要考查了平行线的性质和多边形内角与外角的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°才能正确解答此题.

练习册系列答案
相关题目
【题目】2018年国家将扩大公共场所免费上网范围,某小区响应号召调查小区居民上网费用情况,随机抽查了30户家庭的月上网费用,结果如表
月网费(元) | 50 | 100 | 150 |
户数(人) | 15 | 12 | 3 |
则关于这30户家庭的月上网费用,中位数是_____.