题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,点D在AB上,将△BCD绕点C按顺时针方向旋转90°后得△ECF.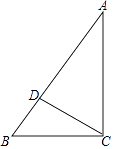
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
【答案】
(1)解:如图所示:△CEF,即为所求;
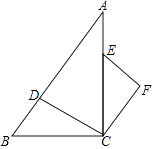
(2)证明:∵EF∥CD,
∴∠FEC=∠ACD.
由旋转的性质可知:∠BCD=∠ECF,∠BDC=∠EFC.
∵∠BCD+∠ACD=90°,
∴∠DCF=∠ACD+∠ECF=∠FEC+∠ECF=90°,
∴∠BDC=∠EFC=180°﹣(∠FEC+∠ECF)=90°.
【解析】(1)画出旋转后的△CEF即可;
(2)由EF∥CD可得出∠FEC=∠ACD,根据旋转的性质可知∠BCD=∠ECF、∠BDC=∠EFC,结合∠BCD+∠ACD=90°即可得出∠FEC+∠ECF=90°,再根据三角形内角和定理即可求出∠EFC=90°,此题得证.
【考点精析】根据题目的已知条件,利用平行线的性质的相关知识可以得到问题的答案,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目