题目内容
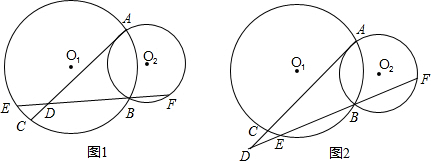
已知:⊙O1与⊙O2外切于点P,过点P的直线分别交⊙O1、⊙O2于点B、A,⊙O1的切线BN交⊙O2于点M、N,AC为⊙O2的弦.(1)如图(1),设弦AC交BN于点D,求证:AP•AB=AC•AD;
(2)如图(2),当弦AC绕点A旋转,弦AC的延长线交直线BN于点D时,试问:AP•AB=AC•AD是否仍然成立?证明你的结论.

分析:(1)过点P作两圆的切线EF,连接CP并延长交⊙O1于点G,连接BG.根据弦切角定理可以证明∠C=∠B,从而证明△APC∽△ADB,再根据相似三角形的性质即可证明;
(2)过点P作两圆的切线EF,连接NP并延长交⊙O1于点G,连接BG.根据弦切角定理和三角形的外角的性质证明∠APC=∠D,从而根据两角对应相等得到△APC∽△ADB,再根据相似三角形的性质即可证明.
(2)过点P作两圆的切线EF,连接NP并延长交⊙O1于点G,连接BG.根据弦切角定理和三角形的外角的性质证明∠APC=∠D,从而根据两角对应相等得到△APC∽△ADB,再根据相似三角形的性质即可证明.
解答: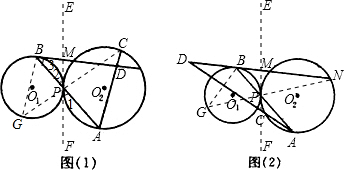
解:(1)过点P作两圆的切线EF,连接CP并延长交⊙O1于点G,连接BG.
∴∠1=∠C,∠2=∠G.
∵⊙O1的切线BN交⊙O2于点M、N,
∴∠3=∠G.
又∠1=∠2,
∴∠C=∠3.
又∠CAP=∠BAD,
∴△APC∽△ADB.
∴
=
,
即AP•AB=AC•AD.
(2)过点P作两圆的切线EF,连接NP并延长交⊙O1于点G,连接BG.连接CP,
则∠APF=∠BPE=∠PBN=∠D+∠A,∠CPF=∠A,
则∠APC=∠D.
又∠PAC=∠DAB,
∴△APC∽△ADB.
∴
=
,
即AP•AB=AC•AD.

解:(1)过点P作两圆的切线EF,连接CP并延长交⊙O1于点G,连接BG.
∴∠1=∠C,∠2=∠G.
∵⊙O1的切线BN交⊙O2于点M、N,
∴∠3=∠G.
又∠1=∠2,
∴∠C=∠3.
又∠CAP=∠BAD,
∴△APC∽△ADB.
∴
| AP |
| AD |
| AC |
| AB |
即AP•AB=AC•AD.
(2)过点P作两圆的切线EF,连接NP并延长交⊙O1于点G,连接BG.连接CP,
则∠APF=∠BPE=∠PBN=∠D+∠A,∠CPF=∠A,
则∠APC=∠D.
又∠PAC=∠DAB,
∴△APC∽△ADB.
∴
| AP |
| AD |
| AC |
| AB |
即AP•AB=AC•AD.
点评:作两圆的公切线是相切两圆中常见的辅助线之一.熟练运用弦切角定理、相似三角形的判定和性质.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 11、如图,已知:⊙O1与⊙O2是等圆,它们相交于A、B两点,O2在⊙O1上,AC是⊙O2的直径,直线CB交⊙O1于D,E为AB延长线上一点,连接DE.
11、如图,已知:⊙O1与⊙O2是等圆,它们相交于A、B两点,O2在⊙O1上,AC是⊙O2的直径,直线CB交⊙O1于D,E为AB延长线上一点,连接DE.