题目内容
 如图所示,在直线l上有若干个点A1、A2、…、An,每相邻两点之间的距离都为1,点P是线段A1An上的一个动点.
如图所示,在直线l上有若干个点A1、A2、…、An,每相邻两点之间的距离都为1,点P是线段A1An上的一个动点.(1)当n=3时,则点P分别到点A1、A2、A3的距离之和的最小值是
2
2
;(2)当n=13时,则当点P在点
A7
A7
的位置时,点P分别到点A1、A2、…、A13的距离之和有最小值,且最小值是42
42
.分析:(1)根据线段的中点到线段两端点的距离最小,可得P在A2处,根据PA1+PA3,可得最小值;
(2)根据线段的中点到线段两端点的距离最小,可得P在A7处,根据各条线段的距离和,可得最小值.
(2)根据线段的中点到线段两端点的距离最小,可得P在A7处,根据各条线段的距离和,可得最小值.
解答:解:(1)P在A2处,PA1+PA3=1+1=2,;
(2)当点P在点 A7的位置时,(PA1+PA2+PA3+PA4+PA5+PA6)×2
=(1+2+3+4+5+6)×2=42,
故答案为:2,A7,42.
(2)当点P在点 A7的位置时,(PA1+PA2+PA3+PA4+PA5+PA6)×2
=(1+2+3+4+5+6)×2=42,
故答案为:2,A7,42.
点评:本题考查了绝对值,线段的中点到线段两端点的距离最小,P分别处于线段的中点,可得最小值.

练习册系列答案
相关题目
 17、如图所示,在直线l上有若干个点A1、A2、…、An,每相邻两点之间的距离都为1,点P是线段A1An上的一个动点.
17、如图所示,在直线l上有若干个点A1、A2、…、An,每相邻两点之间的距离都为1,点P是线段A1An上的一个动点.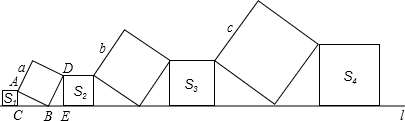
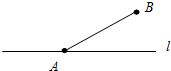 如图所示,在直线l上找到一点P,使△PAB为等腰三角形,请问这样的P点有
如图所示,在直线l上找到一点P,使△PAB为等腰三角形,请问这样的P点有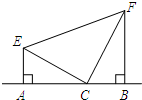 如图所示,在直线AB上有一点C,过点A作AE⊥AB,垂足为A,过点B作BF⊥AB,垂足为B,且AE=BC,BF=AC,连接EF.
如图所示,在直线AB上有一点C,过点A作AE⊥AB,垂足为A,过点B作BF⊥AB,垂足为B,且AE=BC,BF=AC,连接EF.