题目内容
如图所示，在直线l上依次摆放着七个正方形，已知S1=1，S2=2，S3=3，S4=4，另外三个正方形的边长分别为a，b，c．（1）图中Rt△ABC与
| AC2+BC2 |
（2）用上述（1）中思路求b、c的值．（提示：△ABC与△BDE的斜边相等，并且有一个角是直角，只需设一个锐角相等即可）
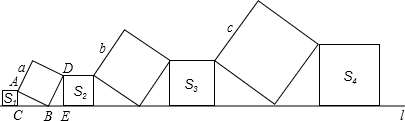
分析：由S1=1，S2=2，可得AC=1，a=
．同理可求b、c的值．
| 3 |
解答：解：（1）∵七个正方形，
∴AB=BD．
∠DBE=∠BAC，
∠BDE=∠ABC，
∴△ABC≌△BDE．
∴DE=BC．
∵S1=1，∴AC=1．
∵S2=2，∴a=
；
（2）∵七个正方形，
∴AB=BD．
∠DBE=∠BAC，
∠BDE=∠ABC，
∴△ABC≌△BDE．
∴DE=BC．
∵S1=1，∴AC=1．
∵S2=2，a=
∴b2=S2+S3，
∵S3=3，
∴b=
．
同理c=
．
∴AB=BD．
∠DBE=∠BAC，
∠BDE=∠ABC，
∴△ABC≌△BDE．
∴DE=BC．
∵S1=1，∴AC=1．
∵S2=2，∴a=
| 3 |
（2）∵七个正方形，
∴AB=BD．
∠DBE=∠BAC，
∠BDE=∠ABC，
∴△ABC≌△BDE．
∴DE=BC．
∵S1=1，∴AC=1．
∵S2=2，a=
| 3 |
∴b2=S2+S3，
∵S3=3，
∴b=
| 5 |
同理c=
| 7 |
点评：此题主要是根据全等三角形的判定，证明三角形全等，然后求出结论．
练习册系列答案
相关题目
17、如图所示，在直线l上有若干个点A1、A2、…、An，每相邻两点之间的距离都为1，点P是线段A1An上的一个动点．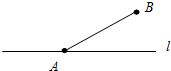
如图所示，在直线l上找到一点P，使△PAB为等腰三角形，请问这样的P点有
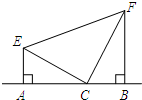如图所示，在直线AB上有一点C，过点A作AE⊥AB，垂足为A，过点B作BF⊥AB，垂足为B，且AE=BC，BF=AC，连接EF．
如图所示，在直线l上有若干个点A1、A2、…、An，每相邻两点之间的距离都为1，点P是线段A1An上的一个动点．