题目内容
已知:![]() ,
,![]() ,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧。
,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧。
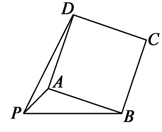
1.(1)如图,当∠APB=45°时,求AB及PD的长;
2.(2)当∠APB变化,且其它条件不变时,求PD 的最大值,及相应∠APB 的大小。
1.(1)①如图11,作AE⊥PB于点E.
∵ △APE中,∠APE=45°,![]() ,
,
∴ 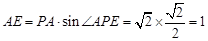 ,
,

![]() .
.
∵ ![]() ,
,
∴  .
.
在Rt△ABE中,∠AEB=90°,
∴ ![]() .…………1分
.…………1分
②解法一:如图12,因为四边形ABCD为正方形,可将
△PAD绕点A顺时针旋转90°得到△![]() ,
,
可得△ ≌△
≌△![]() ,
,![]() ,
,![]() .
.
∴ 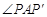 =90°,
=90°,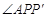 =45°,
=45°,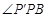 =90°.
=90°.
∴ 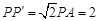 .分
.分
∴ 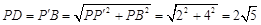 .…………2分
.…………2分
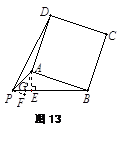 解法二:如图13,过点P作AB的平行线,与DA的延长线交于F,设DA的 延长线交PB于G.
解法二:如图13,过点P作AB的平行线,与DA的延长线交于F,设DA的 延长线交PB于G.
在Rt△AEG中,可得
![]() ,
,
![]() ,
,![]() .
.
在Rt△PFG中,可得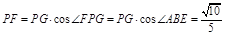 ,
,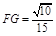 .
.
在Rt△PDF中,可得 ![]()
![]() .
.
2.(2)如图14所示,将△PAD绕点A顺时针旋转90°得到△![]() , PD 的最大值即为
, PD 的最大值即为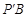 的最大值.
的最大值.
∵ △![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
且P、D两点落在直线AB的两侧,
∴ 当![]() 三点共线时,
三点共线时,![]() 取得最大值(见图15).
取得最大值(见图15).
此时![]() ,即
,即![]() 的最大值为6. …………4分
的最大值为6. …………4分
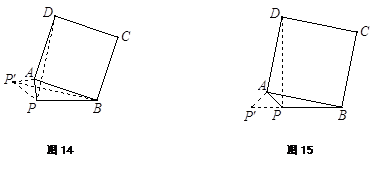 此时∠APB=180°-
此时∠APB=180°-![]() =135°. …………5分
=135°. …………5分
解析:略


 点D在y轴的负半轴上,且点D的坐标为(0,-9),
点D在y轴的负半轴上,且点D的坐标为(0,-9),