题目内容
已知二次函数y=ax2+bx+c(a≠0)的图象经过A(-3,0),B(1,0),C(0,-2),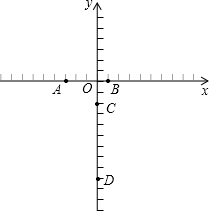 点D在y轴的负半轴上,且点D的坐标为(0,-9),
点D在y轴的负半轴上,且点D的坐标为(0,-9),①求二次函数的解析式.
②点E在①中的抛物线上,四边形ABCE是以AB为一底边的梯形,求点E的坐标.
③在①、②成立的条件下,过点E作直线EF⊥OA,垂足为F,直线EF与线段AD相交于点G,在抛物线上是否存在点P,使直线PG与y轴相交所成的锐角等于梯形ABCE的底角?若存在请求出点P的坐标;若不存在,请说明理由.
分析:①已知函数的图象经过A,B,C三点,把三点的坐标代入解析式就可以得到一个三元一次方程组,就可以求出函数的解析式;
②由题意和图象可知CE∥AB,可求的E点的纵坐标为-2,把-1代入y=
x2+
x-2.可求的点E横坐标.
③首先求得点F的坐标,根据Rt△AFG∽Rt△AOD,则
=
=
,求得G(-2,-3),H(0,-3),根据Rt△AFE≌Rt△BOC,所以AE=BC,所以梯形ABCE是等腰梯形,所以∠BAE=∠ABC.当∠GMH=∠ABC,可以推知Rt△GHM≌Rt△COB,所以HM=OB=1.然后分类讨论:点M在线段OH上和点M在线段HD上,设出直线PG的解析式并求出来,根据P既在PG上,又在抛物线上列出方程组,如果有解,就可以求得点P的坐标,同时说明点P的存在;如果方程组无解,说明点P不存在.
②由题意和图象可知CE∥AB,可求的E点的纵坐标为-2,把-1代入y=
| 2 |
| 3 |
| 4 |
| 3 |
③首先求得点F的坐标,根据Rt△AFG∽Rt△AOD,则
| AF |
| AO |
| FG |
| OD |
| 1 |
| 3 |
解答: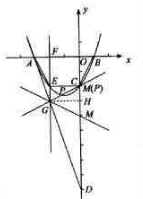 解:①y=ax2+bx+c的图象经过A(-3,0),B(1,0),C(0,-2),三点,
解:①y=ax2+bx+c的图象经过A(-3,0),B(1,0),C(0,-2),三点,
解得:a=
,b=
,c=-2.
∴y=
x2+
x-2.
②由题意和图象可知CE∥AB,
∴E点的纵坐标为-2,
∴-2=
x2+
x-2.
即x2+2x=0,
∴x1=0(舍),x2=-2,
∴E点的坐标为(-2,-2);
③答:存在.
设直线PG与y轴交于点M,过点G作GH⊥OD于H.
∵点G在AD上,GF∥OD,E(-2,-2),
∴F(-2,0).
又∵∠FAG=∠OAD,∠AFG=∠AOD=90°,
∴Rt△AFG∽Rt△AOD,
∴
=
=
.
又∵OD=9,
∴FG=3,
∴G(-2,-3),H(0,-3).
∵AF=BO=1,FE=OC=2,
易证Rt△AFE≌Rt△BOC,
∴AE=BC,
∴梯形ABCE是等腰梯形,
∴∠BAE=∠ABC.当∠GMH=∠ABC,可以推知Rt△GHM≌Rt△COB,
∴HM=OB=1.
①当点M在线段OH上时,则M(0,-2).设P(x1,y1),直线PG的解析式为y=k1x+b1,则
,
解得,k1=
,
则y=
x-2.
∵点P既在PG上,又在抛物线上,
∴
,
解得,
或
,
则P(0,-2)或(-
,-
);
②当点P在线段HD上时,则M(0,-4).
设P(x2,y2),易求直线PG的解析式为y=
x-4.
∵点P既在PG上,又在抛物线上,
∴
,
∴4
+11x2+12=0,
∵△=-71,∴点P不存在.
综上所述,抛物线上存在符合条件的点P有2个,P(0,-2)或(-
,-
).
 解:①y=ax2+bx+c的图象经过A(-3,0),B(1,0),C(0,-2),三点,
解:①y=ax2+bx+c的图象经过A(-3,0),B(1,0),C(0,-2),三点,
|
解得:a=
| 2 |
| 3 |
| 4 |
| 3 |
∴y=
| 2 |
| 3 |
| 4 |
| 3 |
②由题意和图象可知CE∥AB,
∴E点的纵坐标为-2,
∴-2=
| 2 |
| 3 |
| 4 |
| 3 |
即x2+2x=0,
∴x1=0(舍),x2=-2,
∴E点的坐标为(-2,-2);
③答:存在.
设直线PG与y轴交于点M,过点G作GH⊥OD于H.
∵点G在AD上,GF∥OD,E(-2,-2),
∴F(-2,0).
又∵∠FAG=∠OAD,∠AFG=∠AOD=90°,
∴Rt△AFG∽Rt△AOD,
∴
| AF |
| AO |
| FG |
| OD |
| 1 |
| 3 |
又∵OD=9,
∴FG=3,
∴G(-2,-3),H(0,-3).
∵AF=BO=1,FE=OC=2,
易证Rt△AFE≌Rt△BOC,
∴AE=BC,
∴梯形ABCE是等腰梯形,
∴∠BAE=∠ABC.当∠GMH=∠ABC,可以推知Rt△GHM≌Rt△COB,
∴HM=OB=1.
①当点M在线段OH上时,则M(0,-2).设P(x1,y1),直线PG的解析式为y=k1x+b1,则
|
解得,k1=
| 1 |
| 2 |
则y=
| 1 |
| 2 |
∵点P既在PG上,又在抛物线上,
∴
|
解得,
|
|
则P(0,-2)或(-
| 5 |
| 4 |
| 21 |
| 8 |
②当点P在线段HD上时,则M(0,-4).
设P(x2,y2),易求直线PG的解析式为y=
| 1 |
| 2 |
∵点P既在PG上,又在抛物线上,
∴
|
∴4
| x | 2 2 |
∵△=-71,∴点P不存在.
综上所述,抛物线上存在符合条件的点P有2个,P(0,-2)或(-
| 5 |
| 4 |
| 21 |
| 8 |
点评:本题着重考查了待定系数法求二次函数解析式,考查学生分类讨论,数形结合的数学思想方法.综合性强,能力要求极高.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
已知二次函数y=ax+bx+c(a≠0,a,b,c为常数),对称轴为直线x=1,它的部分自变量与函数值y的对应值如下表,写出方程ax2+bx+c=0的一个正数解的近似值________(精确到0.1).
| x | -0.1 | -0.2 | -0.3 | -0.4 |
| y=ax2+bx+c | -0.58 | -0.12 | 0.38 | 0.92 |
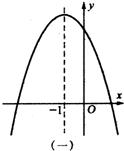 21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
