Question

【题目】如图所示，在Rt△ABC中，∠ACB=90°，∠A=30°，DE垂直平分AC，D为垂足，交AB于E，连接CE．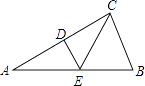
（1）求∠ECB的度数；
（2）若AB=10，求△BCE的周长．

Answer 1

【答案】
（1）解：∵DE垂直平分AC，∠A=30°，

∴AE=CE，∠ACE=∠A=30°，

∵∠ACB=90°，

∴∠BCE=90°﹣30°=60°

（2）解：∵∠ACB=90°，∠A=30°，

∴BC= AB=5，

∴△BCE的周长=CE+BE+BC=AE+BE+BC=AB+BC=15

【解析】（1）根据△ABC中DE垂直平分AC，可求出AE=CE，再根据等腰三角形的性质求出∠ACE=∠A=30°，再根据∠ACB=90°即可解答；（2）根据含30°角的直角三角形的性质得到BC= AB=5，于是得到结论．
【考点精析】本题主要考查了线段垂直平分线的性质的相关知识点，需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等才能正确解答此题．