题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,CE⊥CD且CE=CD,连接EF. 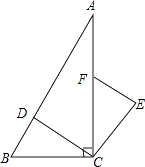
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
【答案】
(1)证明:∵∠ACB=90°,CE⊥CD,
∴∠BCD+∠DCA=90°=∠DCA+∠FCE,
∴∠BCD=∠FCE.
在△BCD和△FCE中, 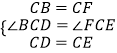 ,
,
∴△BCD≌△FCE(SAS)
(2)解:∵△BCD≌△FCE,
∴∠BDC=∠FEC.
∵EF∥CD,
∴∠DCE+∠FEC=180°,
又∵CE⊥CD,
∴∠FEC=180°﹣∠DCE=180°﹣90°=90°,
∴∠BDC=90°
【解析】(1)根据∠ACB=90°、CE⊥CD利用角的计算即可得出∠BCD=∠FCE,再结合CB=CF、CD=CE即可证出△BCD≌△FCE(SAS);(2)由(1)可得出∠BDC=∠FEC,由EF∥CD利用平行线的性质即可得出∠DCE+∠FEC=180°,再结合CE⊥CD即可得出结论.
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角).

练习册系列答案
相关题目