题目内容
【题目】探索归纳:
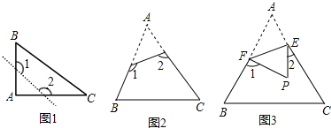
(1)如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于______;
(2)如图2,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=______;
(3)如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是______;
(4)如图3,若没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由.
【答案】(1)270°;(2)220°;(3)∠1+∠2=180°+∠A ;(4)∠1+∠2=2∠A,理由见解析
【解析】
(1)先求出∠B+∠C的度数,再根据四边形内角和等于360°,即可求解;
(2)先求出∠B+∠C的度数,再根据四边形内角和等于360°,即可求解;
(3)先用∠A表示出∠B+∠C,再根据四边形内角和等于360°,即可得到结论;
(4)由折叠的性质得∠AFE=∠PFE,∠AEF=∠PEF,结合平角的定义和三角形内角和定理,即可得到结论.
(1)∵△ABC为直角三角形,∠A=90°,
∴∠B+∠C=180°-90°=90°,
∴∠1+∠2=360°-(∠B+∠C)=270°.
故答案是:270°;
(2)∵△ABC中,∠A=40°,
∴∠B+∠C=180°-40°=140°,
∴∠1+∠2=360°-(∠B+∠C)=220°.
故答案是:220°;
(3)猜想:∠1+∠2=180°+∠A,理由如下:
∵△ABC中,∠B+∠C=180°-∠A,
∴∠1+∠2=360°-(∠B+∠C)=360°-(180°-∠A)=180°+∠A.
故答案是:∠1+∠2=180°+∠A;
(4)∠1+∠2=2∠A,理由如下:
∵△EFP是由△EFA折叠得到的,
∴∠AFE=∠PFE,∠AEF=∠PEF,
∴∠1=180°-2∠AFE,∠2=180°-2∠AEF,
∴∠1+∠2=360°-2(∠AFE+∠AEF),
又∵∠AFE+∠AEF=180°-∠A,
∴∠1+∠2=360°-2(180°-∠A)=2∠A.