Question

【题目】有一张矩形纸片ABCD，，．

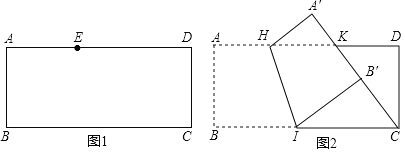
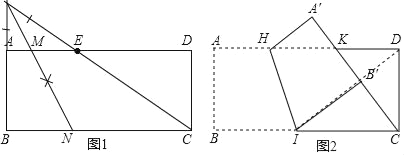
如图1，点E在这张矩形纸片的边AD上，将纸片折叠，使AB落在CE所在直线上，折痕设为点M，N分别在边AD，BC上，利用直尺和圆规画出折痕不写作法，保留作图痕迹；

如图2，点K在这张矩形纸片的边AD上，，将纸片折叠，使AB落在CK所在直线上，折痕为HI，点A，B分别落在点，处，小明认为所在直线恰好经过点D，他的判断是否正确，请说明理由．

Answer 1

【答案】(1)见解析；(2)小明的判断不正确，理由见解析.

【解析】

（1）延长BA交CE的延长线由G，作∠BGC的角平分线交AD于M，交BC于N，直线MN即为所求；

（2）由△CDK∽△IB′C，推出，设CB′＝3k，IB′＝4k，IC＝5k，由折叠可知，IB＝IB′＝4k，可知BC＝BI+IC＝4k+5k＝9，推出k＝1，推出IC＝5，IB′＝4，B′C＝3，在Rt△ICB′中，tan∠B′IC＝，连接ID，在Rt△ICD中，tan∠DIC＝，由此即可判断tan∠B′IC≠tan∠DIC，推出B′I所在的直线不经过点D．

(1)如图1所示直线MN即为所求；

(2)小明的判断不正确，理由如下：

如图2，连接ID，

在Rt△CDK中，∵DK＝3，CD＝4，

∴CK＝＝5，

∵AD∥BC，

∴∠DKC＝∠ICK，

由折叠可知，∠A′B′I＝∠B＝90°，

∴∠IB′C＝90°＝∠D，

∴△CDK∽△IB′C，

∴，

即，

设CB′＝3k，IB′＝4k，IC＝5k，

由折叠可知，IB＝IB′＝4k，

∴BC＝BI+IC＝4k+5k＝9，

∴k＝1，

∴IC＝5，IB′＝4，B′C＝3，

在Rt△ICB′中，tan∠B′IC＝，

连接ID，在Rt△ICD中，tan∠DIC＝，

∴tan∠B′IC≠tan∠DIC，

∴B′I所在的直线不经过点D．