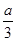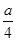题目内容
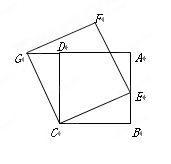
如图,已知正方形 ,点
,点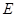 是
是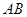 上的一点,连结
上的一点,连结 ,以
,以 为一边,在
为一边,在 的上方作正方形
的上方作正方形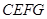 ,连结
,连结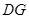 .求证:
.求证: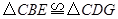 .
.
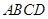 ,点
,点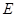 是
是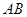 上的一点,连结
上的一点,连结 ,以
,以 为一边,在
为一边,在 的上方作正方形
的上方作正方形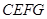 ,连结
,连结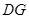 .求证:
.求证: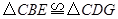 .
.
△CBE≌△CDG.
试题分析:根据正方形性质得出BC=DC,CE=CG,∠BCD=∠ECG=90°,求出∠CBE=∠CDG,根据SAS推出两三角形全等.
试题解析:证明:∵四边形ABCD和四边形CEFG是正方形,
∴BC=DC,CE=CG,∠BCD=∠ECG=90°,
∴∠BCD﹣∠ECD=∠BCD﹣∠ECD,
∴∠BCE=∠DCG,
在△CBE和△CDG中,
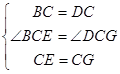 ,
,∴△CBE≌△CDG(SAS).
考点:正方形的性质;全等三角形的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目