题目内容
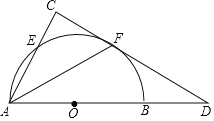
【题目】如图,正方形ABCD的边长为2,点E是边AD的中点,以EC为边作正方形CEFG,则点D与点F之间的距离等于________

【答案】![]() 或
或![]()
【解析】
可分两种情况讨论:①当正方形CEFG在CE的右侧时,如图,过点F作FH⊥AD,交AD的延长线于点H,通过证明△EFH≌△CED求出DH、HF的值,再根据勾股定理求解即可;②当正方形CEFG在CE的左侧时,如图,过点F作FH⊥DA,交DA的延长线于点H,通过证明△EFH≌△CED求出DH、HF的值,再根据勾股定理求解即可.
可分当正方形CEFG在CE的右侧和左侧两种情况讨论:
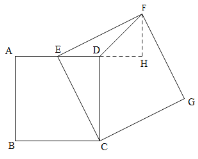
①当正方形CEFG在CE的右侧时,如图,过点F作FH⊥AD,交AD的延长线于点H,
∵E是AD的中点,
∴DE= ![]() AD=1,
AD=1,
∵∠FEC=∠ADC=90°,
∴∠FEH+∠CED=∠CED+∠DCE=90°,
∴∠FEH=∠DCE,
∵∠EHF=∠CDE=90°,CE=EF,
∴△EFH≌△CED(AAS),
∴FH=DE=1,HE=CD=2,
∴HD=1,
∴![]() ;
;
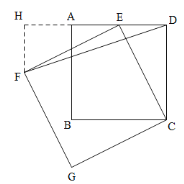
②当正方形CEFG在CE的左侧时,如图,过点F作FH⊥DA,交DA的延长线于点H,
∵E是AD的中点,
∴AE= ![]() AD=1,
AD=1,
∵∠FEC=∠CDE=90°,
∴∠FEH+∠CED=∠CED+∠DCE=90°,
∴∠FEH=∠DCE,
∵∠EHF=∠CDE=90°,CE=EF,
∴△EFH≌△CED(AAS),
∴FH=DE=1,HE=CD=2,
∴HD=HE+DE=3,
∴![]() ;
;
故答案为:![]() 或
或![]() .
.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案【题目】苏州市某初中学校对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成家庭作业时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图的一部分.
时间(小时) | 频数(人数) | 频率 |
0≤t<0.5 | 4 | 0.1 |
0.5≤t<1 | a | 0.3 |
1≤t<1.5 | 10 | 0.25 |
1.5≤t<2 | 8 | b |
2≤t<2.5 | 6 | 0.15 |
合计 | 1 |
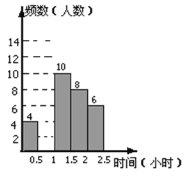
(1)a= ,b= ;
(2)补全频数分布直方图;
(3)请估计该校1 500名初中学生中,约有多少学生在1.5小时以内完成家庭作业.