Question

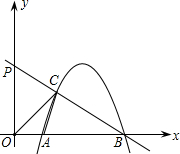如图，抛物线y=ax²-8ax+12a与x轴交于A、B两点，抛物线上有一点C，使∠B=∠OCA，∠ACB=90°，
（1）求OC的长及

BC

AC

的值；
（2）设直线BC与y轴交于P点，点C是BP的中点时，求直线BP和抛物线的解析式．

Answer 1

分析：（1）本题须先令抛物线y=0，可得出A、B的坐标，即可确定OA，OB的长．根据△OCA∽△OBC，可得出关于OC、OA、OB的比例关系式，即可求出OC和及

BC

AC

的值．
（2）本题需根据C是BP中点，因此C的横坐标是B点横坐标的一半，在（1）中已经求得了OC的长，因此不难得出C点的坐标．将C点坐标代入抛物线中即可求出抛物线的解析式．再把B、C点的坐标代入直线的解析式即可结果．

解答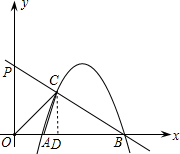：解：（1）由ax²-8ax+12a=0（a＜0）
得x₁=2，x₂=6．
即：OA=2，OB=6．
∵△OCA∽△OBC，
∴OC²=OA•OB=2×6．
∴OC=2

3

或-2

3

（舍去）．
∴线段OC的长为2

3

．
∵△OCA∽△OBC
∴

AC

BC

=

OA

OC

=

2

2 3

=

1

3

∴

BC

AC

=

2 3

2

=

3

（2）设AC=k，则BC=

3

k
∵∠ACB=90°，
∴AC²+BC²=AB²，
则k²+（

3

k）²=（6-2）²
解得k=2（-2舍去）
∴AC=2，BC=2

3

=OC
过点C作CD⊥AB于点D
∴OD=

1

2

OB=3
∴CD=

OC2-OD2

=

3

∴C的坐标为（3，

3

）
将C点的坐标代入抛物线的解析式得

3

=a（3-2）（3-6）
∴a=-

3

3

∴抛物线的函数关系式为：
y=-

3

3

x²+

8 3

3

x-4

3

．
设直线BP的解析式为y=kx+b，
把B、C点的坐标代入得

0=6k+b 3 =3k+b

解得

k=- 3 3 b=2 3

∴直线BP的解析式为y=-

3

3

x+2

3

点评：本题主要考查了二次函数的综合应用，解题时要注意数形结合，综合利用二次函数以及相似三角形的有关知识求二次函数的解析式是本题的关键．