题目内容
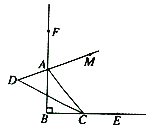
【题目】如图①，在
中，
，
，
是过
点的一条直线，且
、
在的异侧，
于
，
于
.
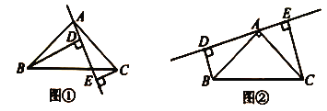
（1）求证：
.
（2）若将直线绕点旋转到图②的位置时（
），其余条件不变，问
与
、
的关系如何？请予以证明.
【答案】（1）见解析；（2）BD=DE-CE，理由见解析.
【解析】
（1）根据已知利用AAS判定△ABD≌△CAE从而得到BD=AE，AD=CE，因为AE=AD+DE，所以BD=DE+CE；
（2）根据已知利用AAS判定△ABD≌△CAE从而得到BD=AE，AD=CE，因为AD+AE=BD+CE，所以BD=DE-CE．
解：（1）∵∠BAC=90°，BD⊥AE，CE⊥AE，
∴∠BDA=∠AEC=90°，
∵∠ABD+∠BAE=90°，∠CAE+∠BAE=90°
∴∠ABD=∠CAE，
∵AB=AC，
在△ABD和△CAE中，
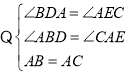
∴△ABD≌△CAE（AAS），
∴BD=AE，AD=CE，
∵AE=AD+DE，
∴BD=DE+CE；
（2）
与
、
的数量关系是BD=DE-CE，理由如下：
∵∠BAC=90°，BD⊥AE，CE⊥AE，
∴∠BDA=∠AEC=90°，
∴∠ABD+∠DAB=∠DAB+∠CAE，
∴∠ABD=∠CAE，
∵AB=AC，
在△ABD和△CAE中，
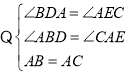
∴△ABD≌△CAE（AAS），
∴BD=AE，AD=CE，
∴AD+AE=BD+CE，
∵DE=BD+CE，
∴BD=DE-CE．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
