题目内容
【题目】综合与探究
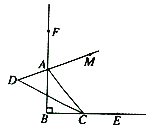
如图所示:点![]() 和点
和点![]() 分别在射线
分别在射线![]() 和射线
和射线![]() 上运动(点
上运动(点![]() 和点
和点![]() 不与点
不与点![]() 重合),
重合),![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 在顶点
在顶点![]() 处的外角平分线,
处的外角平分线,![]() 的反向延长线与
的反向延长线与![]() 交于点
交于点![]() .试回答下列问题:
.试回答下列问题:
(1)若![]() ,则
,则![]() _________
_________![]() ,若
,若![]() ,则
,则![]() _________
_________![]() .
.
(2)设![]() ,用
,用![]() 表示
表示![]() 的度数,则
的度数,则![]() __________
__________![]() .
.
(3)试猜想,点![]() 和点
和点![]() 在运动过程中,
在运动过程中,![]() 的度数是否发生变化?若变化,请求出变化范围;若不变,请给出证明.
的度数是否发生变化?若变化,请求出变化范围;若不变,请给出证明.
【答案】(1)45 45;(2)![]() ;(3)不变,理由如下:
;(3)不变,理由如下:
【解析】
(1)根据角平分线的定义用∠ACB表示出∠ACD,再根据三角形的一个外角等于与它不相邻的两个内角的和与角平分线的定义表示出∠MAC,整理即可得解;
(2)根据(1)可得∠D=45°,然后根据三角形的一个外角等于与它不相邻的两个内角的和解答即可;
(3)根据角的平分线定义表示出∠MAC,∠ACD,再根据三角形的一个外角等于与它不相邻的两个内角的和列式整理即可得到∠D的大小只与∠ABC有关.
(1)∵CD是∠ACB的平分线,
∴∠ACD=![]() ∠ACB,
∠ACB,
∵AM是△ABC在顶点A处的外角平分线,
∴∠MAC=![]() ∠FAC,
∠FAC,
根据三角形外角性质,∠MAC=∠ACD+∠D,
∠FAC=∠ACB+∠ABC,
∴∠ACD+∠D=![]() (∠ACB+∠ABC),
(∠ACB+∠ABC),
∴![]() ∠ACB+∠D=
∠ACB+∠D=![]() ∠ACB+
∠ACB+![]() ∠ABC,
∠ABC,
∠D=![]() ∠ABC,
∠ABC,
∵BF⊥BE,
∴∠ABC=90°,
∴∠D=![]()
即∠D的大小与∠ACB无关,等于![]() ∠ABC,
∠ABC,
当∠ACB=30°,∠D=45°,∠ACB=70°,∠D=45°;
(2)根据(1)∠D=45°,
∵∠ACD=x,
∴在△ACD中,∠MAC=∠ACD+∠D=(45+x)°;
(3)不变.理由如下:
∵CD是∠ACB的平分线,
∴∠ACD=![]() ∠ACB,
∠ACB,
∵AM是△ABC在顶点A处的外角平分线,
∴∠MAC=![]() ∠FAC,
∠FAC,
根据三角形外角性质,∠MAC=∠ACD+∠D,
∠FAC=∠ACB+∠ABC,
∴∠ACD+∠D=![]() (∠ACB+∠ABC),
(∠ACB+∠ABC),
∴![]() ∠ACB+∠D=
∠ACB+∠D=![]() ∠ACB+
∠ACB+![]() ∠ABC,
∠ABC,
∠D=![]() ∠ABC,
∠ABC,
∵BF⊥BE,
∴∠ABC=90°,
∴∠D=![]() ×90°=45°.
×90°=45°.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案