题目内容
【题目】已知:如图,直线BD分别交射线AE、CF于点B、D,连接A、D和B、C,∠1+∠2=180°,∠A=∠C,AD平分∠BDF,求证: 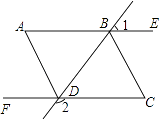
(1)AD∥BC;
(2)BC平分∠DBE.
【答案】
(1)证明:∵∠2+∠BDC=180°,∠1+∠2=180°,
∴∠1=∠DBC,
∴AB∥CF,
∴∠C=∠EBC,
∵∠A=∠C,
∴∠A=∠EBC,
∴AD∥BC;
(2)证明:∵AD平分∠BDF,
∴∠FDA=∠ADB,
∵AD∥BC,
∴∠FDA=∠C,∠ADB=∠DBC,
∵∠C=∠EBC,
∴∠EBC=∠DBC,
∴BC平分∠DBE.
【解析】(1)求出∠1=∠DBC,根据平行线的判定得出AB∥CF,根据平行线的性质得出∠C=∠EBC,求出∠A=∠EBC,根据平行线的判定得出即可;(2)根据角平分线定义求出∠FDA=∠ADB,根据平行线的性质得出∠FDA=∠C,∠ADB=∠DBC,∠C=∠EBC,求出∠EBC=∠DBC即可.
【考点精析】根据题目的已知条件,利用平行线的判定与性质的相关知识可以得到问题的答案,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.

练习册系列答案
相关题目