题目内容
【题目】抛物线![]() 与
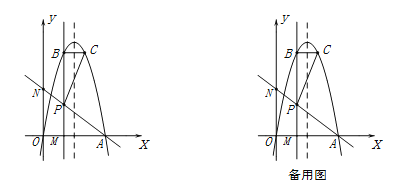
与![]() 轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C不重合),连接AP交y轴于点N,连接BC和PC.
轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C不重合),连接AP交y轴于点N,连接BC和PC.
(1)![]() 时,求抛物线的解析式和BC的长;
时,求抛物线的解析式和BC的长;
(2)如图![]() 时,若AP⊥PC,求
时,若AP⊥PC,求![]() 的值;
的值;
(3)是否存在实数![]() ,使
,使![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ,BC=2;(2)
,BC=2;(2)![]() ;(3)
;(3)![]() ..
..
【解析】
试题分析:(1)由抛物线![]() 与
与![]() 轴相交于O、A两点(其中O为坐标原点),得到b=0,故抛物线为
轴相交于O、A两点(其中O为坐标原点),得到b=0,故抛物线为![]() ,把
,把![]() 代入,得到P(2,3)和
代入,得到P(2,3)和![]() ,由对称轴x=2,即可得到BC的长;
,由对称轴x=2,即可得到BC的长;
(2)把x=2代入![]() ,得到B(2,
,得到B(2,![]() ),设C(x,
),设C(x, ![]() ),由对称轴
),由对称轴![]() ,得到C(
,得到C(![]() ,
, ![]() ),由
),由![]() ,得到A(4a,0),由AP⊥PC,得到
,得到A(4a,0),由AP⊥PC,得到![]() ,即
,即![]() ,解方程即可得到结论;
,解方程即可得到结论;
(3)由OA=4a, OM=2,得到AM=4a-2,由PM∥ON ,得到![]() , 即
, 即![]() ,解方程即可得到结论.
,解方程即可得到结论.
试题解析:(1)∵抛物线![]() 与
与![]() 轴相交于O、A两点(其中O为坐标原点),∴b=0,∴
轴相交于O、A两点(其中O为坐标原点),∴b=0,∴![]() ,当
,当![]() 时,P(2,3),
时,P(2,3),![]() ,∴
,∴![]() =
=![]() ,∴对称轴为:x=2,∴BC=2×(3-2)=2;
,∴对称轴为:x=2,∴BC=2×(3-2)=2;
(2)当x=2时,![]() =
=![]() ,∴B(2,
,∴B(2,![]() ),设C(x,
),设C(x, ![]() ),∵对称轴
),∵对称轴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴C(
,∴C(![]() ,
, ![]() ),∵
),∵![]() ,∴A(4a,0),∵AP⊥PC,∴
,∴A(4a,0),∵AP⊥PC,∴![]() ,∴
,∴![]() ,整理得:
,整理得:![]() ,解得:
,解得:![]() ,∵
,∵![]() ,∴
,∴![]() ;
;
(3)∵A(4a,0),∴OA=4a,∵P(2,2a),∴OM=2,∴AM=4a-2,∵PM∥ON,∴![]() , ∴
, ∴![]() ,解得:
,解得:![]() .
.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目