题目内容
在菱形ABCD中,∠B=60°,点E在射线BC上运动,∠EAF=60°,点F在射线CD上.
(1)当点E在线段BC上时(如图1),求证:EC+CF=AB;
(2)当点E在BC的延长线上时(如图2),线段EC、CF、AB有怎样的相等关系?写出你的猜想,不需证明.

(1)当点E在线段BC上时(如图1),求证:EC+CF=AB;
(2)当点E在BC的延长线上时(如图2),线段EC、CF、AB有怎样的相等关系?写出你的猜想,不需证明.

(1)证明:连接AC,如下图所示:
在菱形ABCD中,∠B=60°,∠EAF=60°,△ABC和△ACD为等边三角形,
∴
,
∴△AEC≌△AFD(ASA),
∴EC+CF=DF+CF=CD=AB.
(2)线段EC、CF、AB的关系为:CF-CE=AB.
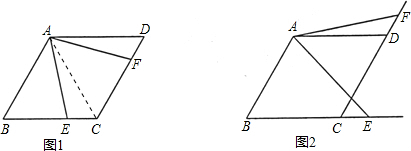
在菱形ABCD中,∠B=60°,∠EAF=60°,△ABC和△ACD为等边三角形,
∴
|
∴△AEC≌△AFD(ASA),
∴EC+CF=DF+CF=CD=AB.
(2)线段EC、CF、AB的关系为:CF-CE=AB.
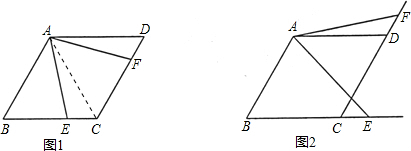

练习册系列答案
相关题目




