题目内容
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:若n=13,则第2018次“F”运算的结果是_____.
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:若n=13,则第2018次“F”运算的结果是_____.
![]()
【答案】1
【解析】
计算出n=13时第一、二、三、四、五、六次运算的结果,找出规律:当次数为偶数时,结果是1;次数是奇数时,结果是4,再进行解答即可.
当n=13时,
第1次“F”运算为:3×13+1=40,
第2次“F”运算为:![]() =5,
=5,
第3次“F”运算为:3×5+1=16,
第4次“F”运算为:![]() =1,
=1,
第5次“F”运算为:1×3+1=4,
第6次“F”运算为:![]() =1
=1
可以看出,从第四次开始,结果就只是1,4两个数轮流出现,且当次数为偶数时,结果是1;次数是奇数时,结果是4,而2018次是偶数,因此最后结果是1.

练习册系列答案
相关题目
【题目】问题:探究函数![]() 的图象与性质.
的图象与性质.
小明根据学习函数的经验,对函数![]() 的图象与性质进行了研究.
的图象与性质进行了研究.
下面是小明的研究过程,请补充完成.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
| … | -4 | -3 | -2 | -1 | 0 |
|
|
| 4 | … |
| … | 2 | 1 | 0 | n | 0 | 1 | m | 3 | 4 | … |
其中,m= n= ;
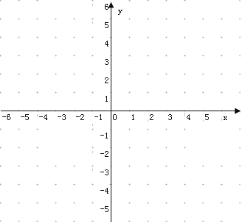
(2)在如图所示的平面直角坐标中,描出以上表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象.
(3)观察图象,写出该函数的两条性质.