题目内容
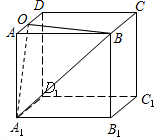 如图,正方体的棱长为2,O为AD的中点,则O,A1,B三点为顶点的三角形面积为
如图,正方体的棱长为2,O为AD的中点,则O,A1,B三点为顶点的三角形面积为分析:在直角△AA1O和直角△OBA中,利用勾股定理可以得到OA1和OB的值,在直角△A1AB中利用勾股定理可得A1B,要求△OA1B1的面积可以通过点O作高,交A1B与M,在Rt△OA1B中求得OM=
A1B=
后,直接求解即可.
| 1 |
| 2 |
| 2 |
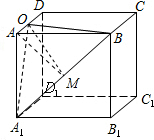
解答:解:直角△AA1O和直角△OBA中,利用勾股定理可以得到OA1=OB=
,
在直角△A1AB中,利用勾股定理得A1B=2
,
过点O作高,交A1B与M,连接AM,
则△AOM是直角三角形,则AM=
A1B=
,
OM=
=
,
∴△OA1B的面积是
A1B•OM=
.
| 5 |

在直角△A1AB中,利用勾股定理得A1B=2
| 2 |
过点O作高,交A1B与M,连接AM,
则△AOM是直角三角形,则AM=
| 1 |
| 2 |
| 2 |
OM=
| OA2+AM2 |
| 3 |
∴△OA1B的面积是
| 1 |
| 2 |
| 6 |
点评:本题主要考查了勾股定理,正确找出图形中的直角三角形,是解决的关键,考查空间想象能力.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
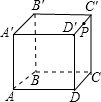 如图,正方体的棱长为2,一只蚂蚁沿正方体的表面从A点爬到C′D′中点P的位置,则蚂蚁爬行的最短路径长为
如图,正方体的棱长为2,一只蚂蚁沿正方体的表面从A点爬到C′D′中点P的位置,则蚂蚁爬行的最短路径长为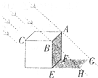 20、如图,正方体的棱长为1米,平行光线垂直于AB,且与BC成45°角,则图中阴影部分(四边形EFGH)的面积为
20、如图,正方体的棱长为1米,平行光线垂直于AB,且与BC成45°角,则图中阴影部分(四边形EFGH)的面积为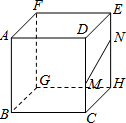 如图,正方体的棱长为3,点M,N分别在CD,HE上,CM=
如图,正方体的棱长为3,点M,N分别在CD,HE上,CM=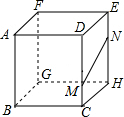 如图,正方体的棱长为3,点M,N分别在CD,HE上,CM=
如图,正方体的棱长为3,点M,N分别在CD,HE上,CM=