题目内容
 如图,△ABC与△ADE是两个全等的等腰三角形,∠C=∠AED=90°,下列说法中正确的是
如图,△ABC与△ADE是两个全等的等腰三角形,∠C=∠AED=90°,下列说法中正确的是
- A.△ABC以A点为旋转中心,顺时针旋转90°与△ADE重合
- B.△ABC以E点为旋转中心,逆时针旋转90°与△ADE重合
- C.△ABC以A点为旋转中心,逆时针旋转45°与△ADE重合
- D.△ABC以A点为旋转中心,逆时针旋转90°与△ADE重合
C
分析:先根据△ABC与△ADE是两个全等的等腰三角形,∠C=∠AED=90°可知AC=BC=AE=DE,AD=AB,再由图形旋转的性质进行解答即可.
解答:∵△ABC与△ADE是两个全等的等腰三角形,∠C=∠AED=90°,
∴AC=BC=AE=DE,AD=AB,
∴∠DAE=∠BAC=45°,
∴△ABC以A点为旋转中心,逆时针旋转45°与△ADE重合,
∴C正确,A、B、D错误.
故选C.
点评:本题考查的是旋转的性质及等腰直角三角形的性质,熟知图形旋转后所得图形与原图形全等是解答此题的关键.
分析:先根据△ABC与△ADE是两个全等的等腰三角形,∠C=∠AED=90°可知AC=BC=AE=DE,AD=AB,再由图形旋转的性质进行解答即可.
解答:∵△ABC与△ADE是两个全等的等腰三角形,∠C=∠AED=90°,
∴AC=BC=AE=DE,AD=AB,
∴∠DAE=∠BAC=45°,
∴△ABC以A点为旋转中心,逆时针旋转45°与△ADE重合,
∴C正确,A、B、D错误.
故选C.
点评:本题考查的是旋转的性质及等腰直角三角形的性质,熟知图形旋转后所得图形与原图形全等是解答此题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
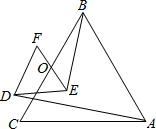 如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为( )
如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为( )A、
| ||
B、
| ||
| C、5:3 | ||
| D、不确定 |
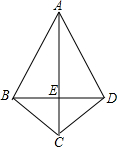 如图,△ABC与△ADC关于直线AC对称,连接BD,若已知四边形ABCD的面积是125,AC=25,则BD的长为
如图,△ABC与△ADC关于直线AC对称,连接BD,若已知四边形ABCD的面积是125,AC=25,则BD的长为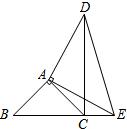 22、如图,△ABC与△ADE是两个大小不同的等腰直角三角形,B、C、E在同一条直线上,连接CD.
22、如图,△ABC与△ADE是两个大小不同的等腰直角三角形,B、C、E在同一条直线上,连接CD.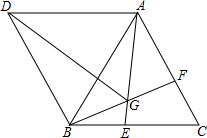 如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.
如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.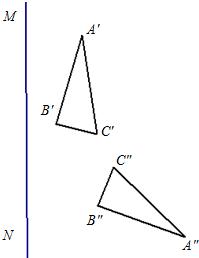 29、如图,△ABC与△A′B′C′关于直线MN对称,△A′B′C′与△A″B″C″关于直线EF对称.
29、如图,△ABC与△A′B′C′关于直线MN对称,△A′B′C′与△A″B″C″关于直线EF对称.