题目内容
 29、如图,△ABC与△A′B′C′关于直线MN对称,△A′B′C′与△A″B″C″关于直线EF对称.
29、如图,△ABC与△A′B′C′关于直线MN对称,△A′B′C′与△A″B″C″关于直线EF对称.(1)画出△ABC和直线EF;
(2)若直线MN和EF相交于点O,直线MN、EF所夹的锐角设为α,猜想∠BOB″与α之间的数量关系,并说明理由.
分析:(1)找到并连接关键点,作出关键点的连线的垂直平分线;(2)根据对称找到相等的角,然后进行推理.
解答: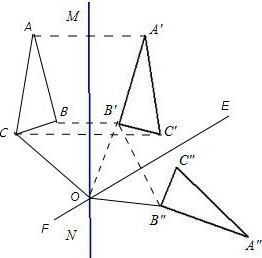 解:(1)如图,连接B′B″.
解:(1)如图,连接B′B″.
作线段B'B″的垂直平分线EF.
则直线EF是△A′B′C′和△A″B″C″的对称轴.
(2)连接B′O.
∵△ABC和△A'B'C'关于MN对称,
∴∠BOM=∠B'OM.
又∵△A'B'C'和△A″B″C″关于EF对称,
∴∠B′OE=∠B″OE.
∴∠BOB″=∠BOM+∠B′OM+∠B′OE+∠B″OE=2(∠B′OM+∠B′OE)=2α
即∠BOB″=2α.
 解:(1)如图,连接B′B″.
解:(1)如图,连接B′B″.作线段B'B″的垂直平分线EF.
则直线EF是△A′B′C′和△A″B″C″的对称轴.
(2)连接B′O.
∵△ABC和△A'B'C'关于MN对称,
∴∠BOM=∠B'OM.
又∵△A'B'C'和△A″B″C″关于EF对称,
∴∠B′OE=∠B″OE.
∴∠BOB″=∠BOM+∠B′OM+∠B′OE+∠B″OE=2(∠B′OM+∠B′OE)=2α
即∠BOB″=2α.
点评:本题考查了轴对称变换作图及轴对称得性质,解答此题要明确轴对称的性质:1.对称轴是一条直线.2.垂直并且平分一条线段的直线称为这条线段的垂直平分线,或中垂线.线段垂直平分线上的点到线段两端的距离相等.3.在轴对称图形中,对称轴两侧的对应点到对称轴两侧的距离相等.4.在轴对称图形中,对称轴把图形分成完全相等的两份.5.如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
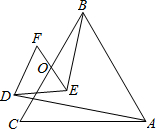 如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为( )
如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为( )A、
| ||
B、
| ||
| C、5:3 | ||
| D、不确定 |
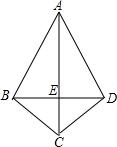 如图,△ABC与△ADC关于直线AC对称,连接BD,若已知四边形ABCD的面积是125,AC=25,则BD的长为
如图,△ABC与△ADC关于直线AC对称,连接BD,若已知四边形ABCD的面积是125,AC=25,则BD的长为 22、如图,△ABC与△ADE是两个大小不同的等腰直角三角形,B、C、E在同一条直线上,连接CD.
22、如图,△ABC与△ADE是两个大小不同的等腰直角三角形,B、C、E在同一条直线上,连接CD.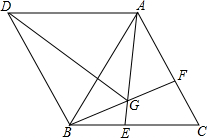 如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.
如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.