题目内容
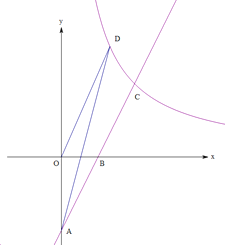
【题目】如图1,已知点A(0,9),B(24,9),C(22+3 ![]() ,0),半圆P的直径MN=6
,0),半圆P的直径MN=6 ![]() ,且P,A重合时,点M,N在AB上,过点C的直线l与x轴的夹角α为60°.现点P从A出发以每秒1个单位长度的速度向B运动,与此同时,半圆P以每秒15°的速度绕点P顺时针旋转,直线l以每秒1个单位长度的速度沿x轴负方向运动(与x轴的交点为Q).当P、B重合时,半圆P与直线l停止运动.设点P的运动时间为t秒.
,且P,A重合时,点M,N在AB上,过点C的直线l与x轴的夹角α为60°.现点P从A出发以每秒1个单位长度的速度向B运动,与此同时,半圆P以每秒15°的速度绕点P顺时针旋转,直线l以每秒1个单位长度的速度沿x轴负方向运动(与x轴的交点为Q).当P、B重合时,半圆P与直线l停止运动.设点P的运动时间为t秒. 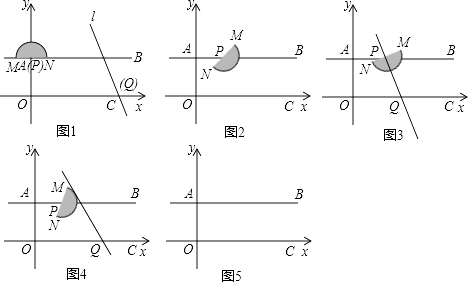
【发现】
(1)点N距x轴的最近距离为 , 此时,PA的长为;
(2)t=9时,MN所在直线是否经过原点?请说明理由.
(3)如图3,当点P在直线l时,求直线l分半圆P所成两部分的面积比. 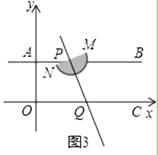
(4)【拓展】如图4,当半圆P在直线左侧,且与直线l相切时,求点P的坐标. 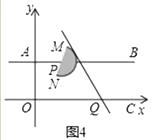
(5)【探究】求出直线l与半圆P有公共点的时间有多长?
【答案】
(1)9﹣3 ![]() ;6
;6
(2)解:MN所在直线经过原点,
理由:当t=9时,∠APN=180°﹣9×15°=45°,AP=9×1=9,
设此时直线MN交y轴于点D,
则AD=APtan45°=9×1=9,
又OA=9,
所以点D与点O重合,即MN所在直线经过原点
(3)解:如图1,

当点P在直线l上时,过点P作PH⊥x轴,垂足为H,
∴OQ=OH+QH=AP+ ![]() =t+
=t+ ![]() =3
=3 ![]() +t,
+t,
∴CQ=t,
∵OQ+CQ=3 ![]() +t+t=OC=22+3
+t+t=OC=22+3 ![]() ,得t=11,
,得t=11,
此时,∠APN=180°﹣11×15°=15°,
∠NPQ=180°﹣15°﹣60°=105°,
∠MPQ=180°﹣105°=75°,
∴S左:S右=105:75=7:5;
(4)解:如图2,

设直线l与AB交于点E,与半圆P相切于点T,
则PT=3 ![]() ,PE=
,PE= ![]() =
= ![]() =6,AE=AP+PE=t+6,
=6,AE=AP+PE=t+6,
过点E作EF⊥x轴,垂足为F,
则OQ=OF+FQ=AE+ ![]() =(t+6)+
=(t+6)+ ![]() =6+3
=6+3 ![]() +t,
+t,
CQ=t,
由OQ+CQ=6+3 ![]() +t+t=OC=22+3
+t+t=OC=22+3 ![]() ,得t=8,
,得t=8,
此时,点P的坐标为(8,9);
(5)解:当半圆P在直线右侧,且与直线l相切时,如图3所示,

设直线l与AB交于点G,与半圆P相切于点R,
则PR=3 ![]() ,PG=
,PG= ![]() =
= ![]() =6,AG=AP﹣PG=t﹣6,
=6,AG=AP﹣PG=t﹣6,
过点G作GJ⊥x轴,垂足为J,
则OQ=OJ+JQ=AG+ ![]() =(t﹣6)+
=(t﹣6)+ ![]() =3
=3 ![]() ﹣6+t,
﹣6+t,
CQ=t,
由OQ+CQ=3 ![]() ﹣6+t+t=OC=22+3
﹣6+t+t=OC=22+3 ![]() ,得t=14,
,得t=14,
则直线l与半圆P有公共点的时间为14﹣8=6秒.
【解析】解:发现(1)当PN∥y轴时,点N距x轴的最近,
∵A(0,9),
∴OA=9,
∵MN=6 ![]() ,
,
∴PN= ![]() MN=3
MN=3 ![]() ,
,
∴点N距x轴的最近距离为9﹣3 ![]() ,
,
此时∠APN=90°,
∴t= ![]() =6,
=6,
∴PA的长为6;
所以答案是:9﹣3 ![]() ,6;
,6;

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
1 | ° | x | 7 | ﹣3 | … |
(1)可知x= ,= ,°= ;
(2)试判断第2016个格子中的数是多少?并给出相应的理由.
(3)判断:前n个格子中所填整数之和是否可能为2016?若能,求出n的值,若不能,请说明理由.