题目内容
【题目】如图,已知l1∥l2 , AC、BC、AD为三条角平分线,则图中与∠1互为余角的角有( ) 
A.1个
B.2个
C.3个
D.4个
【答案】D
【解析】解:∵l1∥l2 , 且AC、BC、AD为三条角平分线, ∴∠1+∠2= ![]() ×180°=90°,
×180°=90°,
∴∠1与∠2互余,
又∵∠2=∠3,
∴∠1与∠3互余,
∵∠CAD=∠1+∠4= ![]() ×180°=90°,
×180°=90°,
∴∠1与∠4互余,
又∵∠4=∠5,
∴∠1与∠5互余,
故与∠1互余的角共有4个.
故选:D.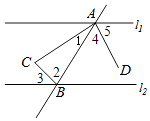
【考点精析】利用角的平分线和平行线的性质对题目进行判断即可得到答案,需要熟知从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
相关题目
【题目】为保护学生视力,课桌椅的高度都是按一定的关系配套设计的,研究表明:假设课桌的高度为ycm,椅子的高度为xcm,则y应是x 的一次函数,下表列出两套符合条件的课桌椅的高度:
第一套 | 第二套 | |
椅子高度xcm | 40 | 37 |
桌子高度ycm | 75 | 70 |
(1)请确定y与x的函数关系式;
(2)现有一把高39cm的椅子和一张高为72.8的课桌,它们是否配套?为什么?