题目内容
 如图,等边三角形△OPQ的边长为2,Q在x轴正半轴上,若反比例函数y=
如图,等边三角形△OPQ的边长为2,Q在x轴正半轴上,若反比例函数y=| k |
| x |
| 3 |
| 3 |
分析:根据等边三角形的性质得出OP,OH,PH的长,进而得出P点坐标,即可得出k的值.
解答: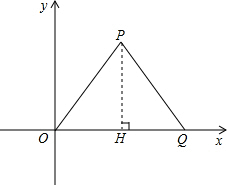 解:过点P作PH⊥OQ于点H,
解:过点P作PH⊥OQ于点H,
∵等边三角形△OPQ的边长为2,
∴OP=2,OH=1,
∴PH=
=
,
∴P点坐标为:(1,
).
则k=xy=
.
故答案为:
.
 解:过点P作PH⊥OQ于点H,
解:过点P作PH⊥OQ于点H,∵等边三角形△OPQ的边长为2,
∴OP=2,OH=1,
∴PH=
| 22-12 |
| 3 |
∴P点坐标为:(1,
| 3 |
则k=xy=
| 3 |
故答案为:
| 3 |
点评:此题主要考查了反比例函数的综合应用,根据已知得出P点坐标是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
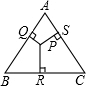 如图,等边三角形ABC内有一点P,过点P向三边作垂线,垂足分别为S、Q、R,且PQ=6,PR=8,PS=10,则△ABC的面积等于( )
如图,等边三角形ABC内有一点P,过点P向三边作垂线,垂足分别为S、Q、R,且PQ=6,PR=8,PS=10,则△ABC的面积等于( )A、190
| ||
B、192
| ||
C、194
| ||
D、196
|
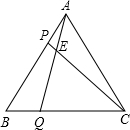 重合),且AP=BQ,AQ、CP相交于点E.
重合),且AP=BQ,AQ、CP相交于点E.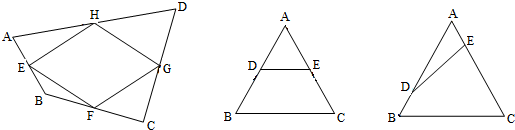
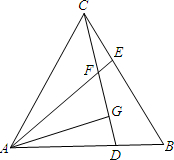 如图,等边三角形ABC中,D、E分别在AB、BC边上,且AD=BE,AE与CD交于点F,AG⊥CD于点G.下列结论:①AE=CD;②∠AFC=120°;③△ADF是正三角形;④
如图,等边三角形ABC中,D、E分别在AB、BC边上,且AD=BE,AE与CD交于点F,AG⊥CD于点G.下列结论:①AE=CD;②∠AFC=120°;③△ADF是正三角形;④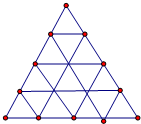 如图把等边三角形各边4等分,分别连接对应点,试计算图中所有的三角形个数是
如图把等边三角形各边4等分,分别连接对应点,试计算图中所有的三角形个数是