题目内容
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A在x轴的正半轴上,顶点C在y轴的正半轴上,OA=12,OC=9,连接AC.
(1)填空:点A的坐标: ;点B的坐标: ;
(2)若CD平分∠ACO,交x轴于D,求点D的坐标;
(3)在(2)的条件下,经过点D的直线交直线BC于E,当△CDE为以CD为底的等腰三角形时,求点E的坐标.

【答案】(1)(12,0),(12,9);(2)D(![]() ,0);(3)E(
,0);(3)E(![]() ,9).
,9).
【解析】
(1)根据矩形的性质即可解决问题;
(2)如图1中,作DM⊥AC于M.由Rt△CDO≌Rt△CDM(HL),推出CM=OC=9,由AC=![]() =15,推出AM=6,设OD=DM=m,在Rt△ADM中,根据AD2=DM2+AM2,构建方程即可解决问题;
=15,推出AM=6,设OD=DM=m,在Rt△ADM中,根据AD2=DM2+AM2,构建方程即可解决问题;
(3)如图2中,作线段CD的中垂线EF,垂足为F,交BC 于E,则EC=ED,△ECD是以CD为底的等腰三角形.想办法求出直线EF的解析式即可解决问题;
解:(1)∵四边形OABC是矩形,
∴AB=OC=9,BC=OA=12,
∴A(12,0),B(12,9),
故答案为(12,0),(12,9);
(2)如图1中,作DM⊥AC于M.
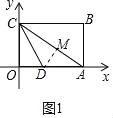
∵DC平分∠ACO,DO⊥CO,DM⊥AC,
∴DO=DM,∠COD=∠CMD=90°,
∵CD=CD,
∴Rt△CDO≌△Rt△CDM(HL),
∴CM=OC=9,
∵AC=![]() =15,
=15,
∴AM=6,设OD=DM=m,
在Rt△ADM中,∵AD2=DM2+AM2,
∴x2+62=(12﹣x)2,
解得x=![]() ,
,
∴D(![]() ,0).
,0).
(3)如图2中,作线段CD的中垂线EF,垂足为F,交BC 于E,则EC=ED,△ECD是以CD为底的等腰三角形.
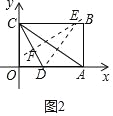
∵C(0,9),D(![]() ,0),
,0),
∴直线CD的解析式为y=﹣2x+9,
∴F(![]() ,
,![]() ),
),
∴直线EF的解析式为y=![]() x+
x+![]() ,
,
当y=9时,x=![]() ,
,
∴E(![]() ,9).
,9).