题目内容
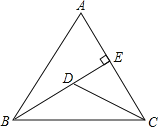
【题目】如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+![]() BD的最小值是( )
BD的最小值是( )
A.2![]() B.4
B.4![]() C.5
C.5![]() D.10
D.10
【答案】B
【解析】
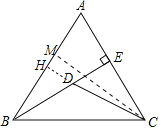
如图,作DH⊥AB于H,CM⊥AB于M.由tanA=![]() =2,设AE=a,BE=2a,利用勾股定理构建方程求出a,再证明DH=
=2,设AE=a,BE=2a,利用勾股定理构建方程求出a,再证明DH=![]() BD,推出CD+
BD,推出CD+![]() BD=CD+DH,由垂线段最短即可解决问题.
BD=CD+DH,由垂线段最短即可解决问题.
解:如图,作DH⊥AB于H,CM⊥AB于M.
∵BE⊥AC,
∴∠AEB=90°,
∵tanA=![]() =2,设AE=a,BE=2a,
=2,设AE=a,BE=2a,
则有:100=a2+4a2,
∴a2=20,
∴a=2![]() 或﹣2
或﹣2![]() (舍弃),
(舍弃),
∴BE=2a=4![]() ,
,
∵AB=AC,BE⊥AC,CM⊥AB,
∴CM=BE=4![]() (等腰三角形两腰上的高相等))
(等腰三角形两腰上的高相等))
∵∠DBH=∠ABE,∠BHD=∠BEA,
∴sin∠DBH=![]() =
=![]() ,
,
∴DH=![]() BD,
BD,
∴CD+![]() BD=CD+DH,
BD=CD+DH,
∴CD+DH≥CM,
∴CD+![]() BD≥4
BD≥4![]() ,
,
∴CD+![]() BD的最小值为4
BD的最小值为4![]() .
.

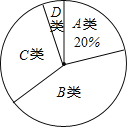
【题目】某校为了解本校九年级男生“引体向上”项目的训练情况,随机抽取该年级部分男生进行了一次测试(满分15分,成绩均记为整数分),按测试成绩m(单位:分)分为A、B、C、D四个组别并绘制出以下两幅不完整的统计图,请根据图中信息解答下列问题:
(1)在被调查的男生中,成绩等级为D的男生有 人,成绩等级为A的男生人数占被调查男生人数的百分比为 %;
(2)本次抽取样本容量为 ,成绩等级为C的男生有 人;
(3)若该校九年级男生有300名,估计成绩少于9分的男生人数.
分组 | 成绩 | 人数 |
A | 12≤m≤15 | 10 |
B | 9≤m≤11 | 22 |
C | 6≤m≤8 | |
D | m≤5 | 3 |
【题目】某网点尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息,如表所示:
销售量n(件) |
|
销售单价m(元/件) |
|
(1)请计算第几天该商品单价为25元/件?
(2)求网店第几天销售额为792元?
(3)求网店销售该商品30天里所获利润y(元)关于x(天)的函数关系式;这30天中第几天获得的利润最大?最大利润是多少?