题目内容
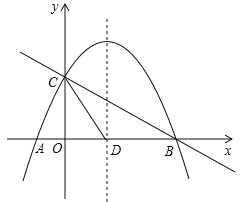
【题目】平面直角坐标系中，点A、B分别在x轴正半轴、y轴正半轴上，AO=BO，△ABO的面积为2.
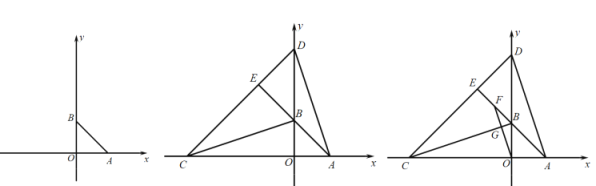
（1）求点A的坐标；
（2）点C、D分别在x轴负半轴、y轴正半轴上（D在B点上方），AD=BC，连接CD交AB延长线于E，设点E横坐标为t，△BCE的面积为S，求S与t的函数关系；
（3）在（2）的条件下，点F为BE中点，连接OF交BC于G，当∠CGO=90°时，求点D坐标.
【答案】（1）A（2,0）；（2）S=t2-2t；（3）D（0,6）.
【解析】
(1) 由△ABO的面积为2.得出方程，求出AO的长度，得出A的坐标；
（2）过E作EM⊥AC于M，可证
，可推出AC、EM、BO的长度，由
，代入即可求出S与t的函数关系式.
（3）由∠CGO=90°可得BC⊥OF，然后根据
列出方程求解即可.
解：（1）∵AO=BO，△ABO的面积为2.
∴
∴AO=2
∴A(2,0)
(2)过E作EM⊥AC于M
∵∠AOB=90°,AO=BO
∴∠BAC=45°
∵∠AOD=∠BOC=90°
∴
∴OC=OD
∵∠COD=90°，OC=OD
∴∠DCO=45°
∴∠BAC=∠DCO=45°
∴CE=EA，∠CEA=90°
∵EM⊥AC
∴M是AC的中点
∵点E横坐标为t
∴OM=|t|=-t
∴AM=2-t
∵∠CEA=90°, M是AC的中点
∴CM=EM=AM=2-t
∴AC=4-2t，OC=2-2t
∵
∴
=
=
=
∴
（3）∵OC=2-2t
∴C(2t-2，0)
∵B(0，2),C(2t-2，0)
∴
∵EM =2-t
∴E(t, 2-t),
∵B(0.2), E(t, 2-t),点F为BE中点
∴F(
)
∵F( ),O(0,0)
∴
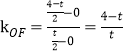
∵∠CGO=90°
∴BC⊥OF
∴
∴
解得：
∵t<0
∴t=-2
∴OC=2-2t=2+4=6
∴OD=OC=6
∴D(0，6).
