题目内容
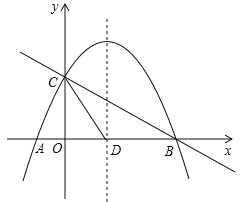
【题目】如图,抛物线![]() 与
与![]() 轴交于A、B两点,与
轴交于A、B两点,与![]() 轴交于点C,抛物线的对称轴交
轴交于点C,抛物线的对称轴交![]() 轴于点D,已知点A(-1,0),点C(0,2).
轴于点D,已知点A(-1,0),点C(0,2).
(1)求抛物线的函数解析式;
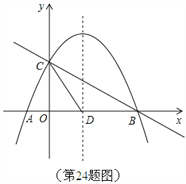
(2)线段BC上有一动点P,过点P作![]() 轴的平行线,交抛物线于点Q,求线段PQ的最大值;
轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)若点E在![]() 轴上,点F在抛物线上.是否存在以C、D、E、F为顶点且以CD为一边的平行四边形?若存在,请你求出点F的坐标;若不存在,请说明理由.
轴上,点F在抛物线上.是否存在以C、D、E、F为顶点且以CD为一边的平行四边形?若存在,请你求出点F的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)当a=2时,PQ有最大值2;(3) 存在3个点符合题意,坐标分别是F1(
;(2)当a=2时,PQ有最大值2;(3) 存在3个点符合题意,坐标分别是F1(![]() )、F2(
)、F2(![]() )、F3(3,2).
)、F3(3,2).
【解析】分析:(1)将点A、C坐标代入求出函数解析式;
(2)先求出直线AB的函数解析式,然后设点P坐标为(a,b),并求出对应的点Q的坐标,然后求出线段PQ的最大值;
(3)本题应分情况讨论:
①将CD平移,令C点落在x轴(即E点)、D点落在抛物线(即F点)上,可根据平行四边形的性质,得出F点纵坐标,代入抛物线的解析式中即可求得F点坐标;
②过C作x轴的平行线,与抛物线的交点符合F点的要求,此时F、C的纵坐标相同,代入抛物线的解析式中即可求出F点坐标.
详解:(1)∵抛物线过点A(-1,0),C(0,2),
∴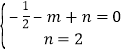 .解得
.解得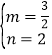 .
.
∴函数解析式为:![]() .
.
(2)由(1)得,![]() ,
,
令![]()
解得x=-1或x=4.∴A(-1,0)、B(4,0).
设直线BC解析式为y=kx+b,它过点B(4,0)、C(0,2),
则有![]() ,解得
,解得![]() .
.
∴直线BC解析式为![]() .
.
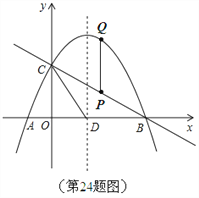
设点P横坐标为a,则点P纵坐标为![]() .
.
∵PQ∥y轴,
∴点Q的横坐标为a,纵坐标为![]() .
.
∴PQ=![]() -(
-(![]() )
)
=![]() =
=![]()
∵![]() ,∴其图象开口向下,有最大值.
,∴其图象开口向下,有最大值.
∴当a=2时,PQ有最大值2.
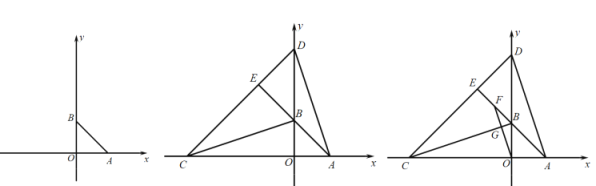
(3)如图所示.
①平移直线CD交x轴于点E,交x轴下方的抛物线于点F.
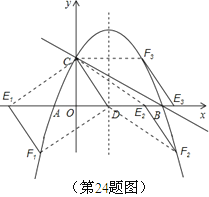
当CD=E1F1时,四边形CDEF为平行四边形.
∵C(0,2),∴设F(x,-2),
代入解析式得:![]() .
.
解得![]() .
.
此时存在点F1(![]() )、F2(
)、F2(![]() )
)
②过点C作CF3∥x轴交抛物线于点F3,过点F3作F3E3∥CD交x
轴于点E3,此时四边形CDE3F3为平行四边形.
此时F3纵坐标为2,将纵坐标代入函数解析式得
![]() .
.
解得:x=0或x=3.
此时存在点F3(3,2).
综上所述,存在3个点符合题意,坐标分别是F1(![]() )、F2(
)、F2(![]() )、F3(3,2).
)、F3(3,2).

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案【题目】为了加强公民的节水意识,合理利用水资源,各地采取价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过![]() 立方米时,水费按每立方米
立方米时,水费按每立方米![]() 元收费,超过
元收费,超过![]() 立方米时,不超过的部分每立方米仍按
立方米时,不超过的部分每立方米仍按![]() 元收费,超过的部分每立方米按
元收费,超过的部分每立方米按![]() 元收费,该市某户今年
元收费,该市某户今年![]() 月份的用水量和所交水费如下表所示:
月份的用水量和所交水费如下表所示:
月份 | 用水量( | 收费(元) |
|
|
|
|
|
|
设某户每月用水量![]() (立方米),应交水费
(立方米),应交水费![]() (元)
(元)
![]() 求
求![]() 的值,当
的值,当![]() 时,分别写出
时,分别写出![]() 与
与![]() 的函数关系式.
的函数关系式.
![]() 若该户
若该户![]() 月份用水量为
月份用水量为![]() 立方米,求该
立方米,求该![]() 月份水费多少元?
月份水费多少元?