题目内容
【题目】(新知理解)
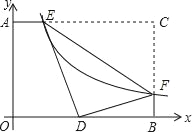
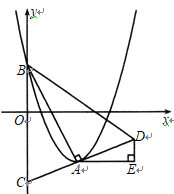
如图1,点![]() 在线段
在线段![]() 上,点
上,点![]() 将线段
将线段![]() 分成两条不相等的线段
分成两条不相等的线段![]() ,
,![]() ,如果较长线段
,如果较长线段![]() 是较短线段
是较短线段![]() 的
的![]() 倍,即
倍,即![]() ,则称点
,则称点![]() 是线段
是线段![]() 的一个圆周率点,此时,线段
的一个圆周率点,此时,线段![]() ,
,![]() 称为互为圆周率伴侣线段.由此可知,一条线段
称为互为圆周率伴侣线段.由此可知,一条线段![]() 的圆周率点有两个,一个在线段
的圆周率点有两个,一个在线段![]() 中点的左侧(如图中点
中点的左侧(如图中点![]() ),另一个在线段
),另一个在线段![]() 中点的右侧.
中点的右侧.
![]()
(1)如图1,若![]() ,则
,则![]() ;若点
;若点![]() 是线段
是线段![]() 的不同于点
的不同于点![]() 的圆周率点,则
的圆周率点,则![]()
![]() (填“
(填“![]() ”或“
”或“![]() ”);
”);
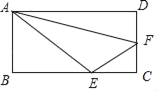
(2)如果线段![]() ,点
,点![]() 是线段
是线段![]() 的圆周率点,则
的圆周率点,则![]() ;
;
(问题探究)
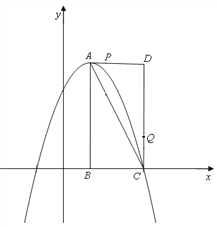
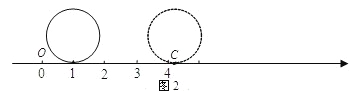
(3)如图2,现有一个直径为1个单位长度的圆片,将圆片上的某点与数轴上表示1的点重合,并把圆片沿数轴向右无滑动的滚动一周,该点到达点![]() 的位置.若点
的位置.若点![]() 是线段
是线段![]() 的两个不同的圆周率点,求线段
的两个不同的圆周率点,求线段![]() 的长;
的长;
(问题解决)
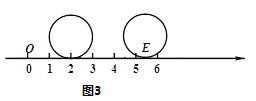
(4)如图3,将直径为1个单位长度的圆片上的某点与数轴上表示2的点重合,并把圆片沿数轴向右无滑动的滚动一周,该点到达点![]() 的位置.若点
的位置.若点![]() 在射线
在射线![]() 上,且线段
上,且线段![]() 与以
与以![]() 、
、![]() 中某两个点为端点的线段互为圆周率伴侣线段,请你直接写出点
中某两个点为端点的线段互为圆周率伴侣线段,请你直接写出点![]() 所表示的数.
所表示的数.
【答案】(1)3π+3,=;(2)5或5 π;(3)MN长为π-1;(4)D点表示的数为:![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
(1)根据圆周率伴侣线段定义得出线段之间的关系,代值求解,根据定义分别得出AC、BD与AB的关系判断AC与BD的关系;(2)根据圆周率点定义,分两种情况,得到AM与BM的关系,代值求解;(3)设OM=x,由定义得MC=πx,根据OC=OM+MC列方程求解;(4)根据点D是线段OE的圆周率点和点E是线段OD的圆周率点,得出四种线段之间的关系,代值求解.
解:(1)∵AC=3,BC=π AC,
∴AB=AC+BC=3π+3;
∵点D、C都是是线段![]() 的圆周率点且不重合,
的圆周率点且不重合,
∴BC=π AC ,AD=πBD,
∴AB=AC+BC=BD+AD,
∴AB=AC+π AC,AB=BD+πBD,
∴AC=![]() ,BD=
,BD=![]() ,
,
∴AC=BD.
(2)设线段AB中点为C,当点M在线段AC之间时,如图1
∵点M是线段![]() 的圆周率点,
的圆周率点,
∴BM=π AM ,
∵![]() ,
,
∴AM+π AM=5+5π
∴AM=5;

当点M在线段BC之间时,如图2
∵点M是线段![]() 的圆周率点,
的圆周率点,
∴AM=π BM ,
∵![]() ,
,
∴π BM+BM=5+5π,
∴BM=5,
∴AM=5 π.
综上所述,AM长为5或5 π.
(3)如图,由题意可知,C点表示的数是π+1,
![]()
M、N均为线段OC的圆周率点,设M点离O点近,且OM=x,
∴MC=πOM=πx
∴x+πx=π+1,
解得x=1,
∴OM=1,
∴OM=CN=1
∴MN=OC-OM-CN=π+1-1-1=π-1.
(4)根据题意得点C表示的数为π+2,设点D表示的数为x,
如图1,若OD=πDE,
∴x=π(π+2-x),
解得,x=![]() ,
,
∴D点表示的数为:![]() ;
;

如图2,若DE=πOD,
∴ π+2-x= πx,
解得,x=![]() ,
,
∴D点表示的数为:![]() ;
;
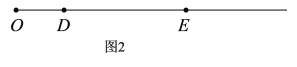
如图3,若OE=πDE,
∴π+2=π(x-π-2),
解得,x=![]() ,
,
∴D点表示的数为:![]() ;
;
如图4,若DE=πOE,
∴x-π-2=π(π+2),
解得,x=![]() ,
,
∴D点表示的数为:![]() .
.
综上所述:D点表示的数为:![]() 或
或![]() 或
或![]() 或
或![]() .
.

【题目】(本题10分)某自行车厂一周计划生产700辆自行车,平均每天生产自行车100辆,由于各种原因,实际每天生产量与计划每天生产量相比有出入。下表是某周的自行车生产情况(超计划生产量为正、不足计划生产量为负,单位:辆):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | +8 | -2 | -3 | +16 | -9 | +10 | -11 |
(1)根据记录可知前三天共生产自行车 辆;
(2)产量最多的一天比产量最少的一天生产 辆;
(3)若该厂实行按生产的自行车数量的多少计工资,即计件工资制。如果每生产一辆自行车就可以得人民币60 元,超额完多成任务,每超一辆可多得 15 元;若不足计划数的,每少生产一辆扣 15 元,那么该厂工人这一周的工资总额是多少?